Numerical Integration using MATLAB

In this tutorial we will compare different methods for integrating a simple differential equation (or model):

\[\dot{x}(t)=u(t)-\frac{1}{2}x(t) \nonumber\]

Assuming $u(t)=1$ at all time (i.e. $u$ is constant), produce plots of $x(t)$ against $t$ from 0 to 10 seconds in the following ways;

Analytically: For this simple example an analytical solution is possible, providing us with a useful reference solution to compare numerical results with, for most models, analytical solutions are very difficult or impossible to find. The analytical solution here is;
\[\int{\frac{1}{1-\frac{x}{2}}dx}=\int{1}dt \nonumber\]
which gives;
\[x(t)=2-2e^{-\frac{1}{2}t} \nonumber\]
Numerically: Now, using MATLAB, write a short script with a for loop over each time step to use the Euler method for integration with a fixed time step h;
\[x(t+h)=x(t)+h\dot{x}(t) \nonumber\]
Clearly you will also need the equation for $\dot{x}(t)$ at the top of this sheet. You do not need to make use of the analytical solution while doing this.
Numerically using Simulink: If you have some experience of using Simulink, you can also write a simple block diagram, and let Simulink do the integration for you (you’ll need an integrator block, a constant block and a sum block).

Given that you know the analytical solution is 100% accurate, compare this with the other method(s). What value of the fixed time step, $h$ is needed for method 2) to give an accurate solution?
Is there any error in the Simulink solution? What if you zoom in to the graph?
Modify your MATLAB script for solving 2), so that it provides mid-point and RK4 (fixed step) integration. Is the solution better?

Your plots should look something like this;

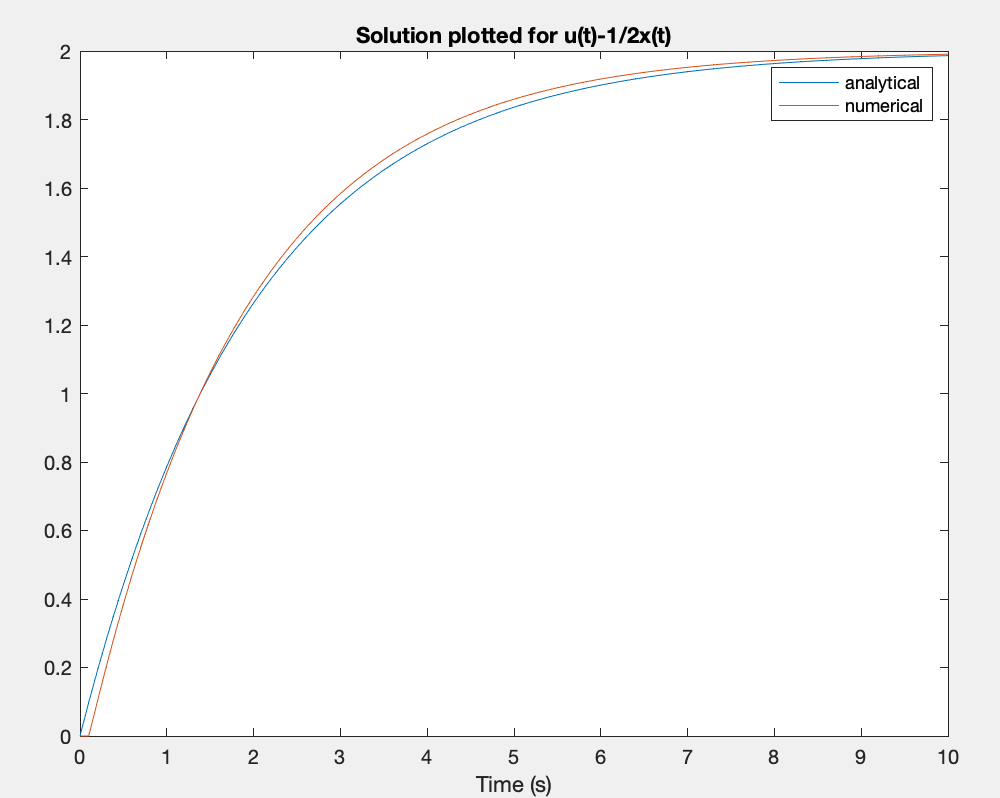
SOLUTION

Please do not play this video until you have tried to do this for yourself!