Dynamic Force Analysis

Single Link in Pure Rotation
Threebar Crank-slide Linkage

Dynamic force analysis enables an engineer to understand more about the forces internal to the mechanism being investigated. This information can be used to improve the design and ensure that it achieves engineering targets.

There are a number of approaches that may be employed for dynamic force analysis however we will be focussing on only one, making use of Newton’s law as defined below in translation.

\[\sum\mathbf{F}=m\mathbf{a} \nonumber\]

and rotation

\[\sum\mathbf{T}=I_g\alpha \nonumber\]

The above equations must be written out for each of the moving bodies in the system which result in a system of equations that can be solved for the unknowns. Typically the weight of the members is ignored since they are often (but not always) negligible compared with the forces imposed on the system as a consequence of its motion (acceleration).

The general approach to a dynamic force analysis is;

Draw a diagram of the system and each of its members, noting on each of the members the coordinate system(s).
Isolate each of the members of the system drawing a free body diagram and noting on this the forces and torques applied to each of the members.
Write out the equations of motion for each of the members and assemble these as a system of equations in matrix form.
Finally, solve the matrix using an appropriate method for the unknowns.

Note that it is often the case that more information about the system will be required to complete the dynamic force analysis, for example the mass, mass moment inertia, angular position and angular speed of the links.

Single Link in Pure Rotation

We will be deriving a system of equations that enable us to calculate forces and torque in a single link undergoing pure rotation.

We are interested in knowing the forces in the single joint and the torque applied, given that we know the length, mass, mass moment of inertia, angle, angular velocity, accelerations and force applied to the link. Therefore, with reference to the diagram below we know the following; $\mathbf{R_{12}}$, $\mathbf{R_{p}}$, $m_2$, $I_{G2}$, $\theta_2$, $\omega_2$, $\alpha_2$, $\alpha_{G_2}$ and $F_P$.

The forces, $F_{12x}$ and $F_{12y}$ as well as the torque, $\mathbf{T_{12}}$ are unknown and this is what we will be calculating. We assume that all unknown forces and torques are positive in direction.

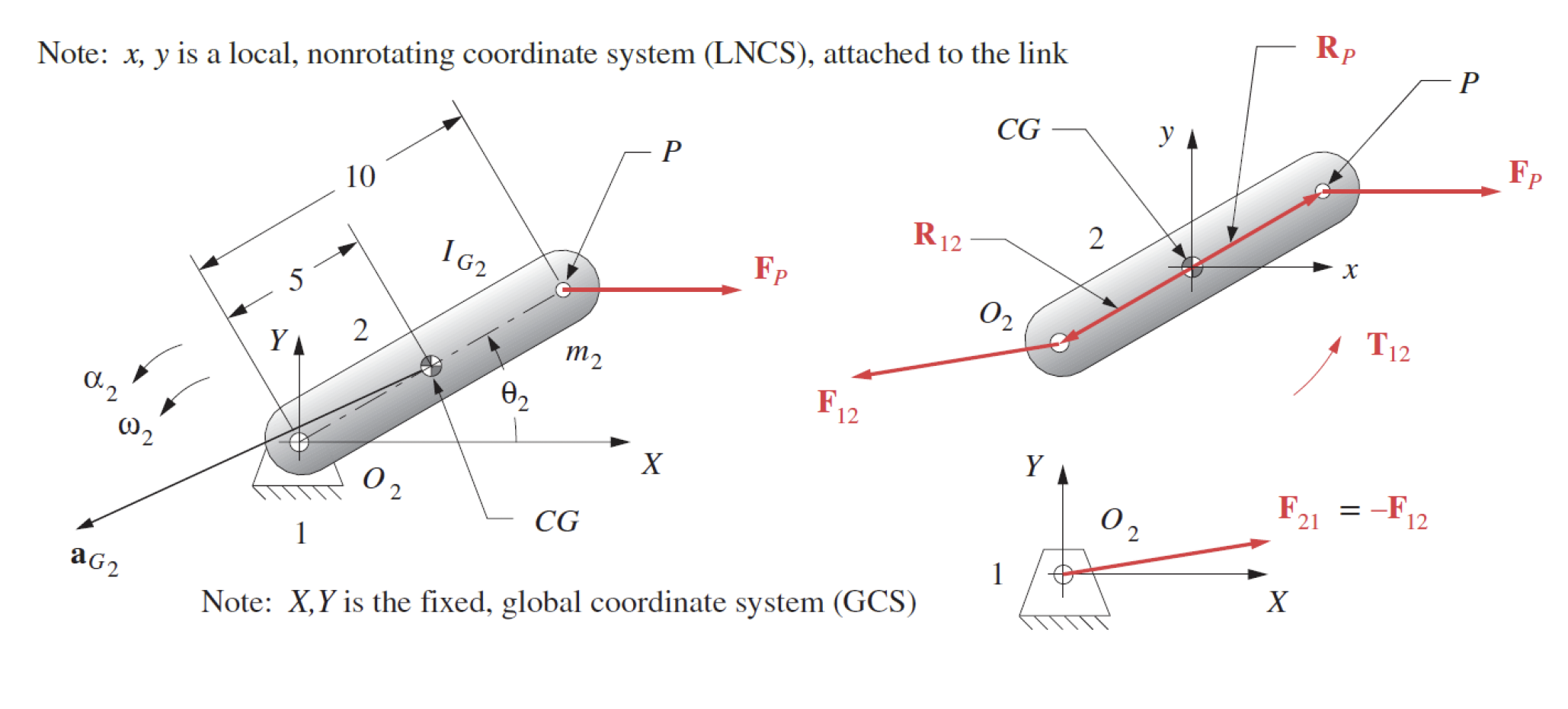
We choose a non-rotating local coordinate system located at the Centre of Gravity (CG) of the link and draw a Free Body Diagram (FBD) as shown in (b) of the figure above.

Note the forces, $\mathbf{F_{12}}$ and $\mathbf{F_p}$ and their point of application, $\mathbf{R_{12}}$ and $\mathbf{R_p}$ respectively.

Note also that there is a Torque, $\mathbf{T_{12}}$ applied to the link at the joint in the counter-clockwise (positive) direction.

We know that we have three unknowns and three equations which means the system can be solved.

Writing out the system of equations.

\[\sum \mathbf{F}=\mathbf{F}_P+\mathbf{F}_{12}=m_2 \mathbf{a}_G \\ \sum \mathbf{T}=\mathbf{T}_{12}+\left(\mathbf{R}_{12} \times \mathbf{F}_{12}\right)+\left(\mathbf{R}_P \times \mathbf{F}_P\right)=I_G \alpha \nonumber\]

Expanding the above remembering that,

\[\mathbf{R} \times \mathbf{F} = (R_x \cdot F_y) - (R_y \cdot F_x) \nonumber\]

the system of equations become

\[\begin{align*} F_{Px} &+ F_{12x} = m_2 a_{Gx} \\ F_{Py} &+ F_{12y} = m_2 a_{Gy} \\ T_{12} &+ \left(R_{12x} F_{12y} - R_{12y} F_{12x}\right) + \left(R_{Px} F_{Py} - R_{Py} F_{Px}\right) = I_G \alpha \end{align*}\]

Putting the equations in matrix form.

\[\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ -R_{12y} & R_{12x} & 1 \end{array}\right] \left[\begin{array}{l} F_{12x} \\ F_{12y} \\ T_{12} \end{array}\right]=\left[\begin{array}{l} m_2 a_{Gx}-F_{Px} \\ m_2 a_{Gy}-F_{Py} \\ I_G \alpha-\left(R_{Px} F_{Py}-R_{Py} F_{Px}\right) \end{array}\right] \nonumber\]

Note that the first matrix on the left contains all of the geometric information about the system and the matrix on the right contains all of the information about the dynamics.

The values of $F_{12x}$, $F_{12y}$ and $T_{12}$ may now be calculated.

Single Link in Pure Rotation - Matlab Code

The following MATLAB code may be used to calculate the unknown values.

% Given scalar parameters
m2 = ; % Mass of the link
IG = ; % Mass moment of inertia
R12x = ; % x-coordinate of the distance from CG of the link to joint
R12y = ; % y-coordinate of the distance from CG of the link to joint
Rp_x = ; % x-coordinate of the distance from CG of the link to force application point
Rp_y = ; % y-coordinate of the distance from CG of the link to force application point
FPx = ; % Force applied along x-axis
FPy = ; % Force applied along y-axis
aGx = ; % Acceleration of CG of the link along x-axis
aGy = ; % Acceleration of CG of the link along y-axis
alpha = ; % Angular acceleration

% Coefficient matrix
A = [1, 0, 0; 
     0, 1, 0; 
     -R12y, R12x, 1];

% Right-hand side of the equations
rhs = [m2 * aGx - FPx; 
       m2 * aGy - FPy; 
       IG * alpha - (Rp_x * FPy - Rp_y * FPx)];

% Solve the system of equations
unknowns = A \ rhs;

% Extracting the unknowns
F12x = unknowns(1);
F12y = unknowns(2);
T12 = unknowns(3);

% Display the results
disp(['F12x = ', num2str(F12x)]);
disp(['F12y = ', num2str(F12y)]);
disp(['T12 = ', num2str(T12)]);

Threebar Crank-slide Linkage

We will be deriving a system of equations that enable us to calculate forces and torque in a threebar crank-slide linkage.

We are interested in knowing the forces at each of the joints and the torque applied, given that we know the length, mass, mass moment of inertia, angle, angular velocity, accelerations of the links and the forces applied. Therefore, with reference to the diagram below we know the following; $\mathbf{R_{12}}$, $\mathbf{R_{32}}$, $\mathbf{R_{23}}$, $\mathbf{R_{13}}$, $\mathbf{R_{p}}$, $m_2$, $m_3$, $I_{g_2}$, $I_{g_3}$, $\theta_2$, $\theta_3$, $\omega_2$, $\omega_3$, $\alpha_2$, $\alpha_3$, $\alpha_{G_2}$, $\alpha_{G_3}$ and $F_P$.

The forces, $\mathbf{F_{12}}$, $\mathbf{F_{32}}$, $\mathbf{F_{13}}$ as well as the torque, $\mathbf{T_{12}}$ are unknown and this is what we will be calculating. We assume that all unknown forces and torques are positive in direction.

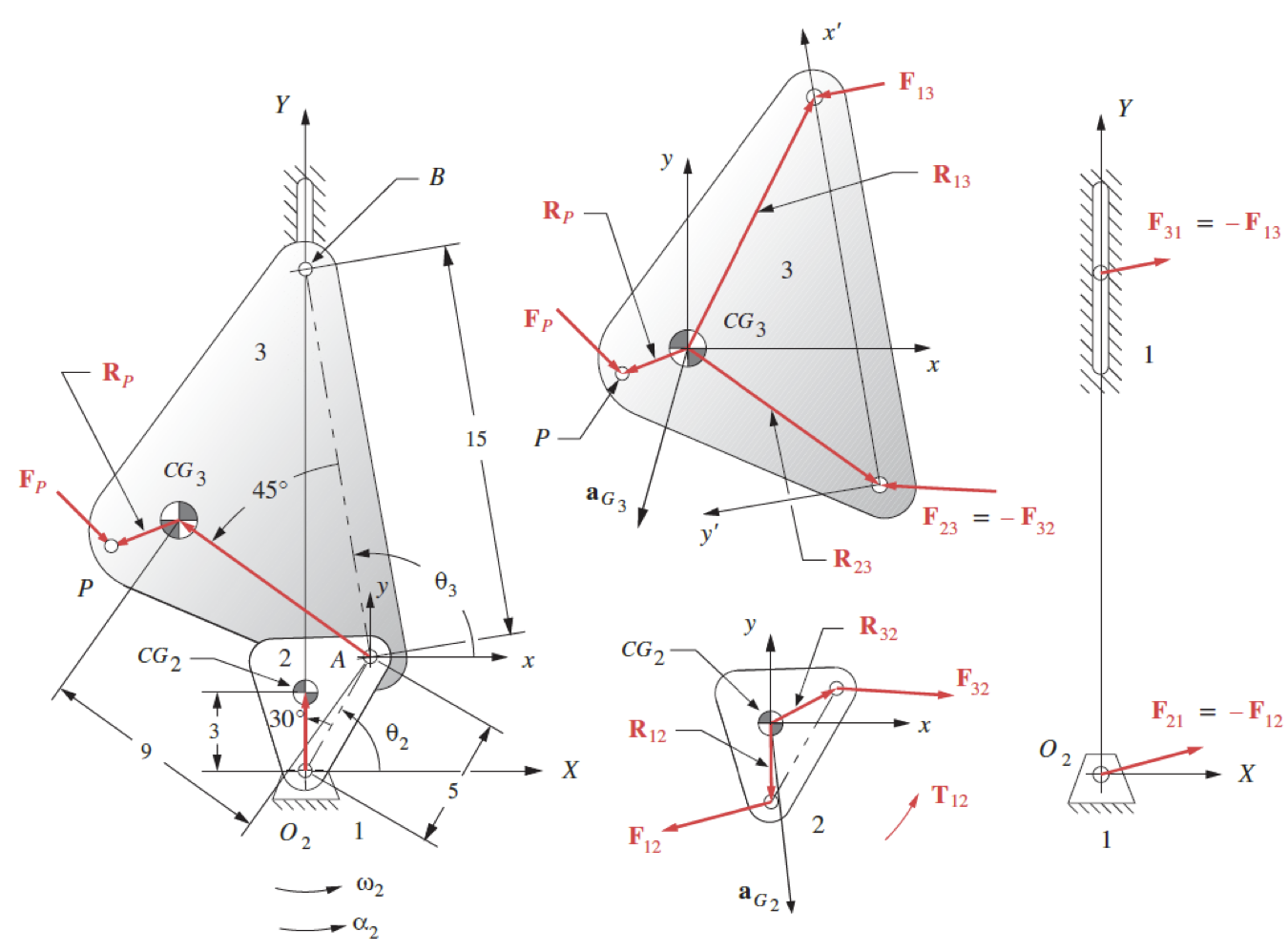
Examine the mechanism in the figure above and compare it with the freebody diagram in the same figure.

As can be seen from the diagram link 1 is the ground and stationary. Link 2 rotates about point $O_2$ resulting in the movement of point $B$ up and down in the vertical direction. Only two of the links move and therefore we should have six equations in six unknowns.

For each of the links in the figure note the forces marked at each of the pin joints and ensure you understand the notation. For example $\mathbf{F_{12}}$ is the force of link 1 (the ground), exerted on link 2, etc.

At the point that link 2 and 3 connect, note the forces, and as we know from Newton’s third law,

\[\mathbf{F_{23}} = -\mathbf{F_{32}} \nonumber\]

Note also the position vectors used to locate the pin joints with respect to the CG in the links nonrotating coordinate system $(xy)$.

An external force, $\mathbf{F_p}$ is applied to link 3 and the position vector $\mathbf{R_p}$ describes its position relative to the nonrotating coordinate system $(xy)$.

For each of the moving links and after the expansion of cross-products, the equations are written, first for link 2,

\[\begin{gathered} F_{12x}+F_{32x}=m_2 a_{G_{2x}} \\ F_{12y}+F_{32y}=m_2 a_{G_{2y}} \\ T_{12}+\left(R_{12x} F_{12y}-R_{12y} F_{12x}\right)+\left(R_{32x} F_{32y}-R_{32y} F_{32x}\right)=I_{G2} \alpha_2 \end{gathered} \nonumber\]

and then for link 3, noting the substitution of the reaction force $-\mathbf{F_{32}}$ for $\mathbf{F_{23}}$ and expansion of the cross-products, the equations are written,

\[\begin{gathered} F_{13x}-F_{32x}+F_{P_x}=m_3 a_{G_{3x}} \\ F_{13y}-F_{32y}+F_{P_y}=m_3 a_{G_{3y}} \\ \left(R_{13x} F_{13y}-R_{13y} F_{13x}\right)-\left(R_{23x} F_{32y}-R_{23y} F_{32x}\right)+\left(R_{P_x} F_{Py}-R_{Py} F_{Px}\right)=I_{G3} \alpha_3 \end{gathered} \nonumber\]

As a result there are seven unknowns, $F_{12x}$, $F_{12y}$, $F_{32x}$, $F_{12y}$, $F_{13x}$, $F_{13y}$ and $T_{12}$, in six equations.

The force $F_{13y}$ is a result of friction at the joint between link 3 and link 1, so we can write,

\[F_{13y} = \mu F_{13x} \nonumber\]

leaving us only six unknowns. Rearranging the equations to put the unknown terms on the right side,

\[\begin{gathered} F_{12x} + F_{32x} = m_2 a_{G_{2x}} \\ F_{12y} + F_{32y} = m_2 a_{G_{2y}} \\ T_{12} + R_{12x} F_{12y} - R_{12y} F_{12x}+R_{32x} F_{32y} - R_{32y} F_{32x} = I_{G_2} \alpha_2 \\ F_{13x} - F_{32x} = m_3 a_{G_{3x}}-F_{P_x} \\ \mu F_{13x} - F_{32y} = m_3 a_{G_{3y}} - F_{P_y} \\ \left( \mu R_{13x} - R_{13y}\right) F_{13x} - R_{23x} F_{32y} + R_{23y} F_{32x} = I_{G3} \alpha_3 - R_{P_x} F_{P_y} + R_{P_y} F_{P_x} \end{gathered} \nonumber\]

and then putting these in matrix form,

\[{\left[\begin{array}{cccccc} 1 & 0 & 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 1 & 0 & 0 \\ -R_{12y} & R_{12x} & -R_{32y} & R_{32x} & 0 & 1 \\ 0 & 0 & -1 & 0 & 1 & 0 \\ 0 & 0 & 0 & -1 & \mu & 0 \\ 0 & 0 & R_{23y} & -R_{23x} & \left(\mu R_{13x}-R_{13y}\right) & 0 \end{array}\right] \times\left[\begin{array}{l} F_{12x} \\ F_{12y} \\ F_{32x} \\ F_{32y} \\ F_{13x} \\ T_{12} \end{array}\right]=} \\ {\left[\begin{array}{c} m_2 a_{G_{2x}} \\ m_2 a_{G_{2y}} \\ I_{G_2} \alpha_2 \\ m_3 a_{G_{3x}}-F_{Px} \\ m_3 a_{G_{3y}}-F_{Py} \\ I_{G_3} \alpha_3-R_{Px} F_{Py}+R_{Py} F_{Px} \end{array}\right]} \\ \nonumber\]

we can solve the system for the six unknowns.

Threebar Crank-slide Linkage - Matlab Code