Week 3 Tutorial - Dynamic Force Analysis
Question 1
The figure shows four linkages and the external forces and torques exerted on or by the linkages in static equilibrium. Sketch the free body diagram of each part of each linkage. Do not attempt to show the magnitudes of the forces, except roughly, but do sketch them in their proper locations and approximate orientations.
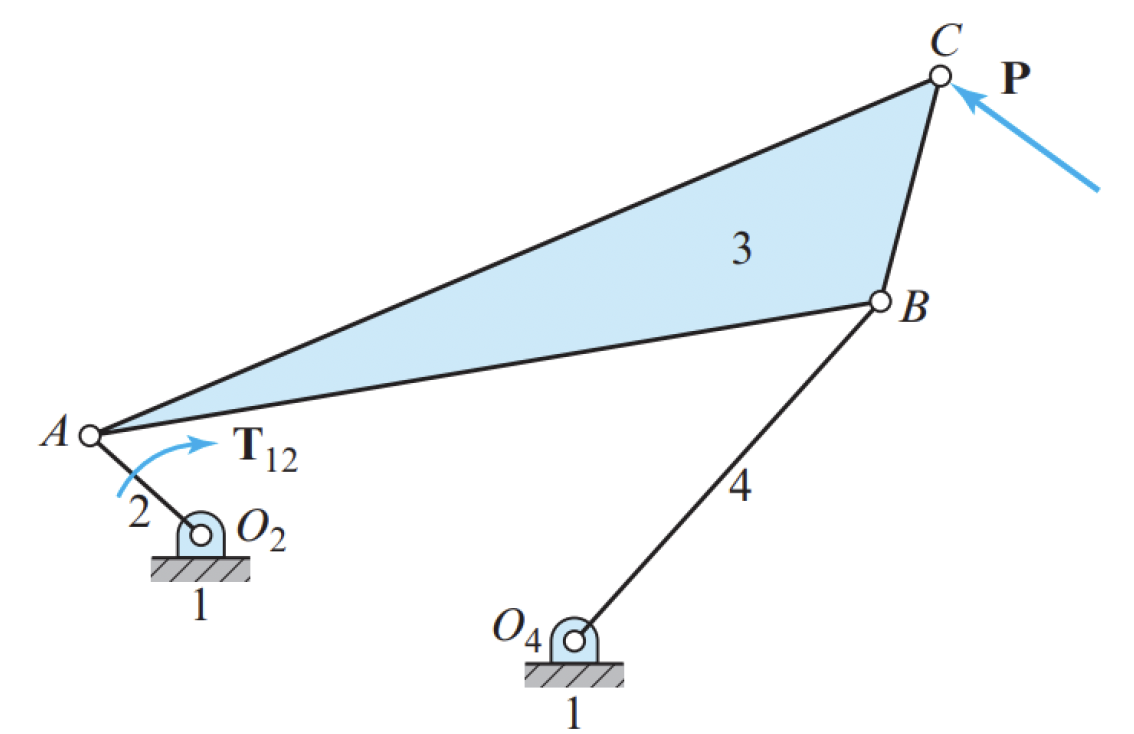
Solution
Link 2
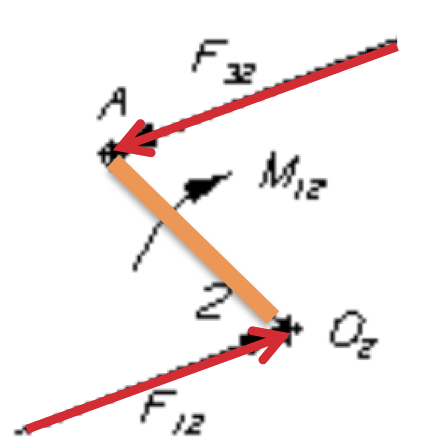
Link 3
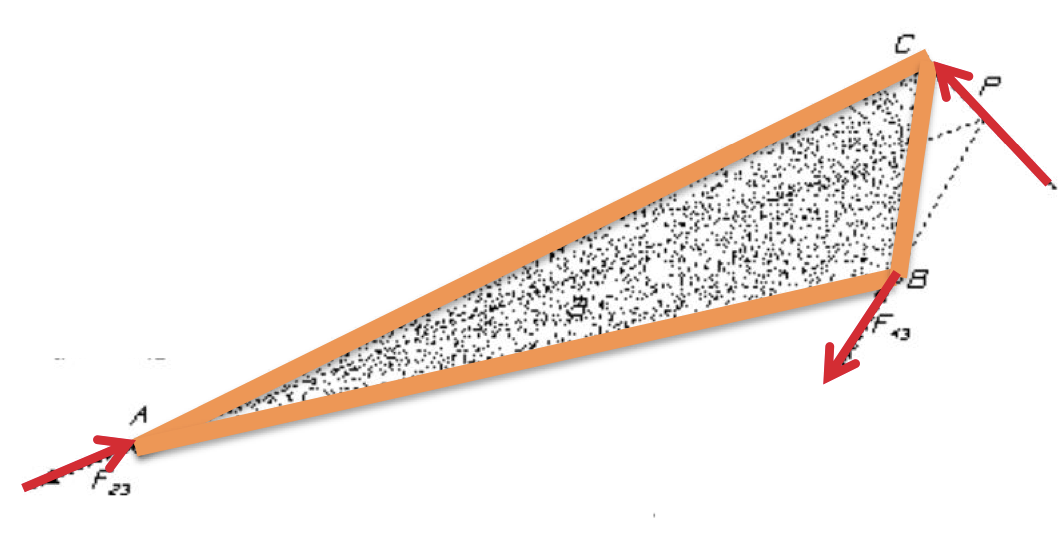
Link 4
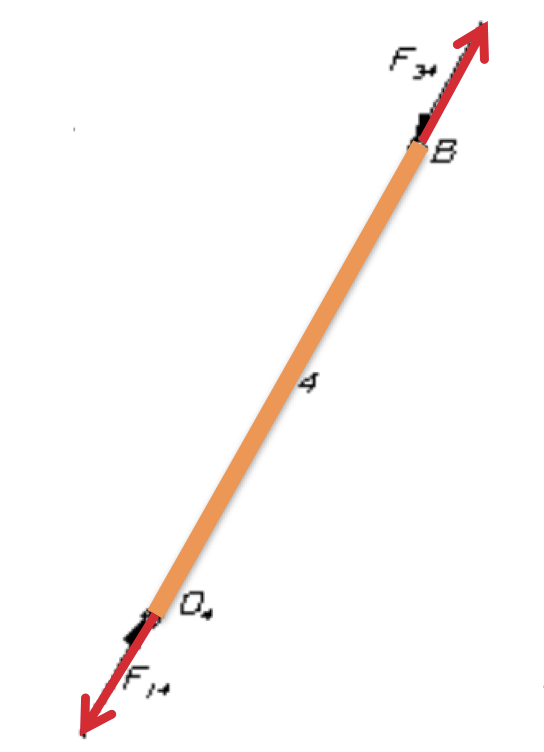
Question 2
Determine the force required by the hydraulic cylinder to maintain the position of the bucket.
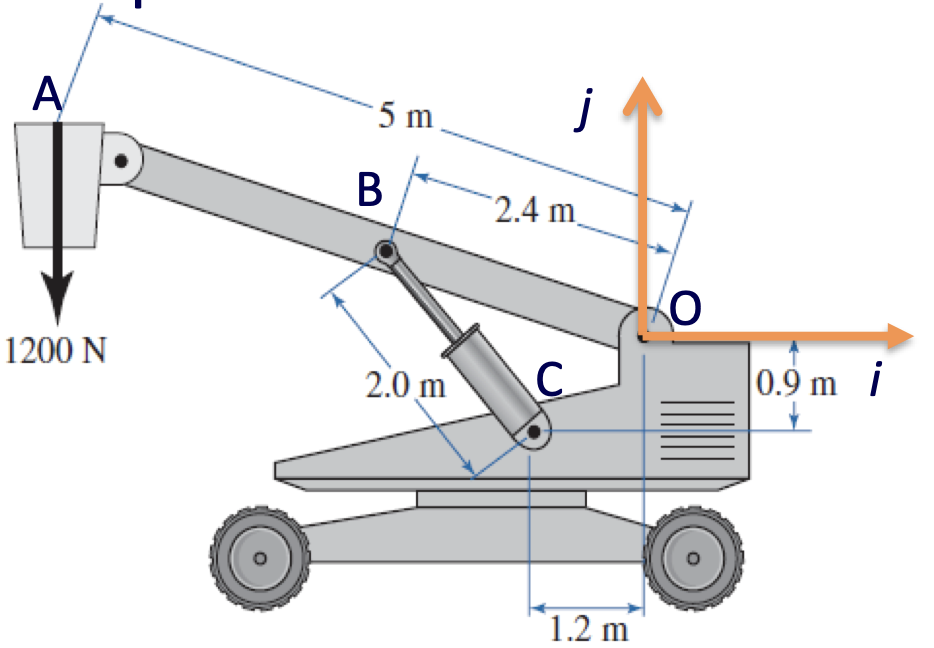
Solution
Step 1
Draw a schematic diagram and choose a coordinate system.
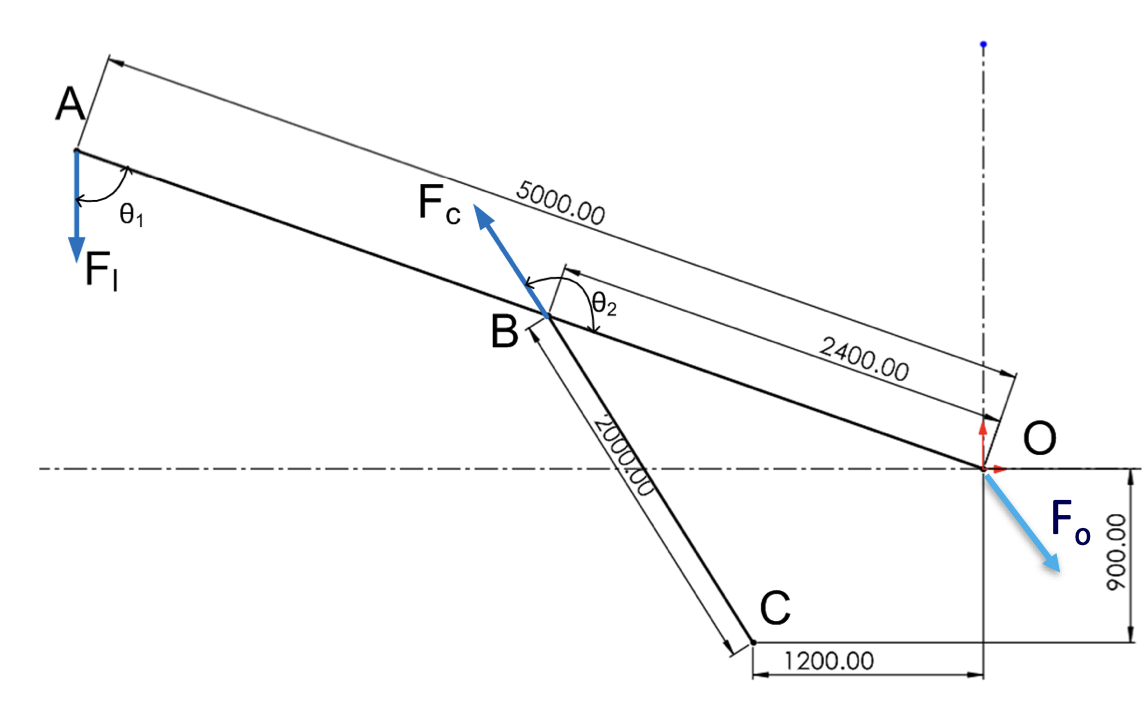
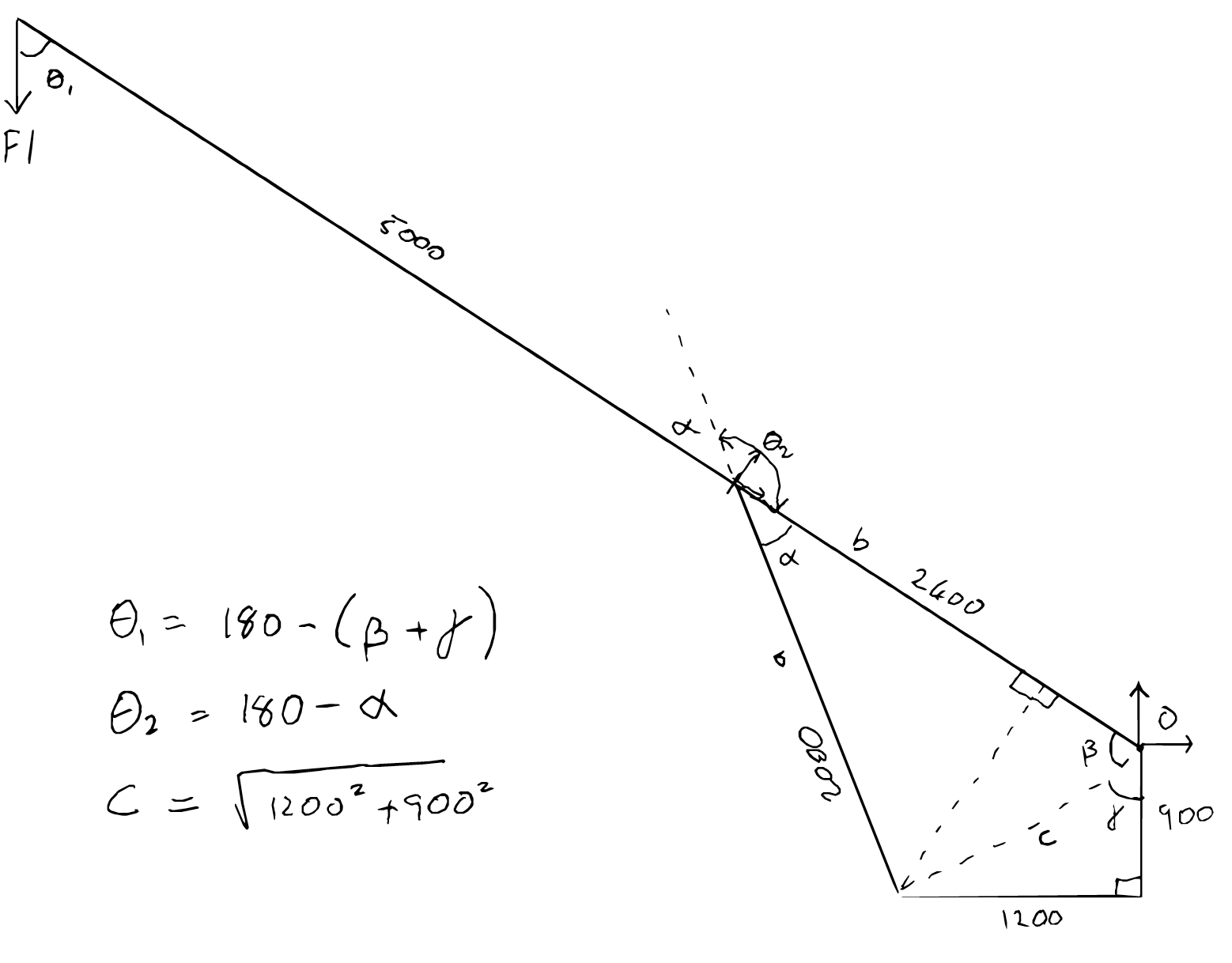
Step 2
Write out the equilibrium equations, taking moments about point O.
\[\sum M_o = R_{AO} \times F_l - R_{BO} \times F_c = 0 \nonumber\]resolving force components
\[\sum M_o = R_{AO} F_l \sin(\theta_1) - R_{BO} F_c \sin(\theta_2) = 0 \nonumber\]Calculate $\theta_1$ and $\theta_2$ by firstly calculating $c$;
\[\begin{align*} c &= \sqrt{1200^2 + 900^2} \\ c &= 1500 \\ \end{align*}\]then calculate $\beta$
\[\begin{align*} \cos{\beta} &= \frac{c^2 + b^2 - a^2}{2bc} \\ \beta &= 56.16^\circ \\[2em] \end{align*}\]then calculate $\alpha$
\[\begin{align*} \cos{\alpha} &= \frac{a^2 + b^2 - c^2}{2ab} \\ \alpha &= 38.53^\circ \\[2em] \end{align*}\]then calculate $\gamma$
\[\begin{align*} \tan \gamma &= \left(\frac{1200}{900}\right) \\ \gamma &= 53.13^\circ \\[2em] \end{align*}\]Finally, calculate $\theta_1$ and $\theta_2$
\[\begin{align*} \theta_1 &= 180 - (\beta + \gamma) \\ &= 70.71^\circ \\[1em] \theta_2 &= 180 - \alpha \\ &= 141.47^\circ \\ \end{align*}\]Step 3
Calculate $F_c$.
\[\begin{align*} F_c &= \frac{R_{AO} F_l \sin(\theta_1)}{R_{BO} \sin(\theta_2)} \\[1em] F_c &= 3788.20 N \end{align*}\]Question 3
Given the force $P = 0.9 kN$, determine the torque $T_{12}$ that is applied to crank 2 to maintain the linkage in static equilibrium where $R_{AO2} = 75mm $ and $R_{BA} = 350mm$.
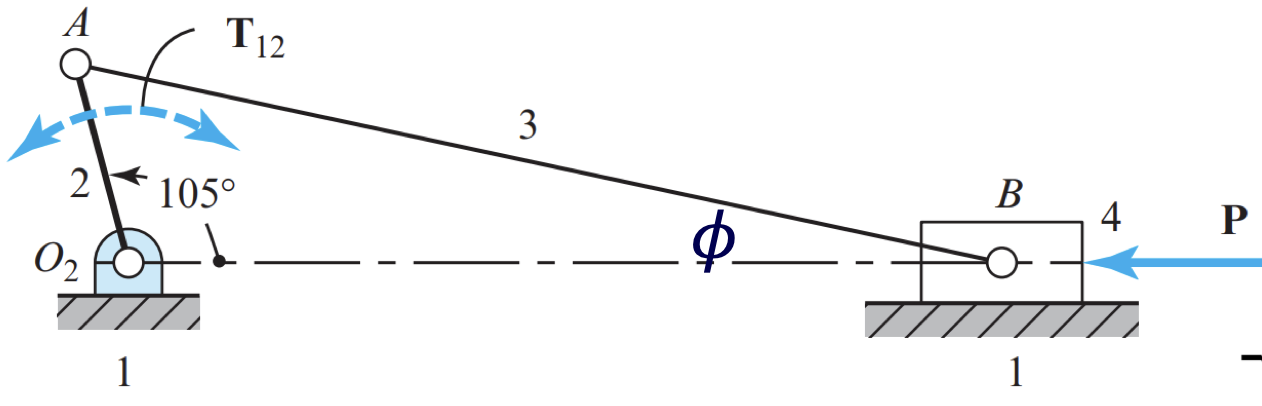
Solution
Step 1
Calculate $\phi$ using the sine law.
\[\begin{align*} &\frac{R_{AO2}}{\sin \phi} = \frac{R_{BA}}{\sin 105} \\[1em] &\phi = \sin^{-1} \left(\frac{R_{AO2}}{R_{BA}} \sin 105\right) \\[1em] &\phi =11.95^\circ \end{align*}\]Step 2
Draw a free body diagram.

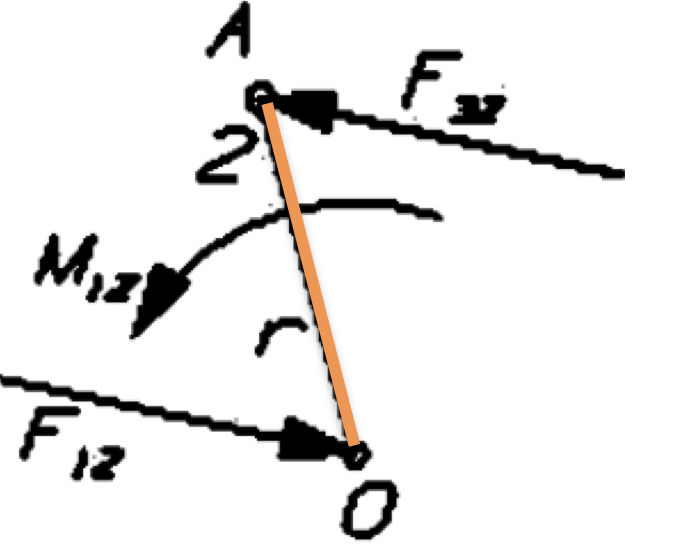
To calculate torque, $T_{12}$ we need to determine the values of $\mathbf{F_{32}}$ and $\mathbf{R_{AO}}$. To do this we first calculate the magnitude of $F_{34}$ and $F_{14}$ as though link 4 is in equilibrium.
\[\begin{align*} &F_{34} \cos \phi - P = 0\\ &F_{34} = 920 N \\[1em] &F_{14} - F_{34} \sin \phi = 0\\ &F_{14} = 189 N \end{align*}\]$\mathbf{F_{32}}$ is equal in magnitude but opposite in direction to $\mathbf{F_{34}}$, so that $\mathbf{F_{32}} = - \mathbf{F_{34}}$
\[\begin{align*} \mathbf{F}_{32} &= -\mathbf{F}_{34} = F_{34} (- \cos \phi \hat{\mathbf{i}} + \sin \phi \hat{\mathbf{j}})\\ \mathbf{F}_{32} &= -\mathbf{F}_{34} = 920(- \cos 11.95 \hat{\mathbf{i}} + \sin 11.95 \hat{\mathbf{j}})\\[1em] \end{align*}\]Finally, before calculating $\mathbf{T_{12}}$ we need to determine $\mathbf{R}_{AO2}$
\[\begin{align*} \mathbf{R}_{AO2} & = R_{AO2} (\cos 105 \hat{\mathbf{i}} + \sin 105 \hat{\mathbf{j}})\\ \mathbf{R}_{AO2} & = 0.075(\cos 105 \hat{\mathbf{i}} + \sin 105 \hat{\mathbf{j}}) \end{align*}\]Calculate $\mathbf{T}_{12}$ as though link 2 and link 3 are in equilibrium.
\[\begin{align*} \mathbf{T}_{12} &= \mathbf{R}_{AO2} \times \mathbf{F}_{32} \\ \mathbf{T}_{12} &= 0.075(\cos 105 \hat{\mathbf{i}} + \sin 105 \hat{\mathbf{j}}) \times 920(-\cos 11.95 \hat{\mathbf{i}} + \sin 11.95 \hat{\mathbf{j}}) \\ \mathbf{T}_{12} &= 61.51 Nm \end{align*}\]Question 4
Determine the reaction forces and the driving torque for the fourbar linkage shown in the diagram below. The input crank is operating at a constant angular velocity, $ω_2 = 48 \ rad/s$ counter-clockwise, and the applied force acting at point $C$ is $F_C = −0.8 \hat{\mathbf{j}} \ kN$. The masses of links 3 and 4 are $m_3 = 1.5 kg$ and $m4 = 5 kg$, respectively, and the second moment of mass of links 2, 3, and 4 are $I_{G2} = 0.025 kg m^2$, $I_{G3} = 0.012 kg m^2$, and $I_{G4} = 0.054 kg m^2$.
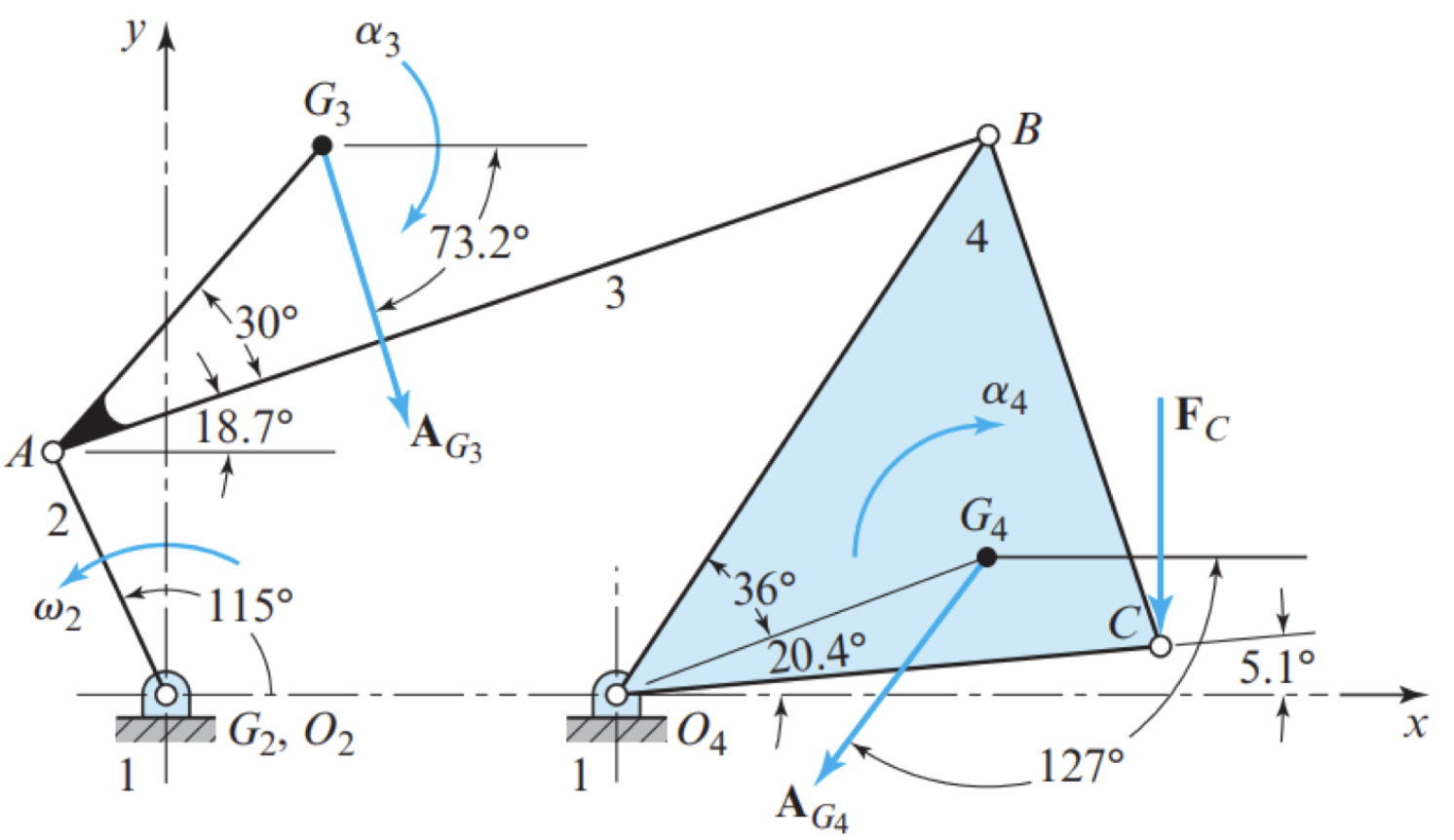
Solution
Step 1
Derive the position vector and the kinematic results, remembering that, $\mathbf{R} = \|\mathbf{R}\| \cos \theta \hat{\mathbf{i}} + \|\mathbf{R}\| \sin \theta \hat{\mathbf{j}}$ where $\|\mathbf{R}\|$ is the magnitude of the vector $\mathbf{R}$
\[\begin{align*} \mathbf{R}_{AO2} &=-25.4 \hat{\mathbf{i}} + 54.4 \hat{\mathbf{j}} \text{ mm} \\ \mathbf{R}_{G3A} &= 59.4 \hat{\mathbf{i}} + 67.6 \hat{\mathbf{j}} \text{ mm} \\ \mathbf{R}_{BA} &= 208.4 \hat{\mathbf{i}} + 70.5 \hat{\mathbf{j}} \text{ mm} \\ \mathbf{R}_{BO4} &= 71.6 \hat{\mathbf{i}} + 131.8 \hat{\mathbf{j}} \text{ mm} \\ \mathbf{R}_{G4O4} &= 81.2 \hat{\mathbf{i}} + 38.7 \hat{\mathbf{j}} \text{ mm} \\ \mathbf{R}_{CO4} &= 119.5 \hat{\mathbf{i}} + 10.7 \hat{\mathbf{j}} \text{ mm} \\ \mathbf{R}_{O4O2} &= 100.0 \hat{\mathbf{i}} \text{ mm} \end{align*}\]Refer to Position Analysis, Velocity Analysis and Acceleration Analysis to obtain acceleration results as follows;
| Variable | Value |
|---|---|
| $\alpha_3$ | -118.9k rad/s² |
| $\alpha_4$ | -625.1k rad/s² |
| $A_{G3}$ | $46.6 \hat{\mathbf{i}} - 154.9 \hat{\mathbf{j}}$ |
| $A_{G4}$ | $-62.6 \hat{\mathbf{i}} - 83.3 \hat{\mathbf{j}}$ |
Step 2
Consider the sum of moments about $A$
\[\begin{align*} \sum \mathbf{M}_A = \mathbf{R}_{G3A} \times (-m_3 \mathbf{A}_{G3}) + (-I_{G3} \mathbf{\alpha}_3) + \mathbf{R}_{BA} \times \mathbf{F}_{43} = 0 \end{align*}\]to obtain the following
\[\begin{align*} \sum \mathbf{M}_A = (0.0705 F_{34x} - 0.2084F_{34y} + 19.96) \hat{\mathbf{k}} \end{align*}\]Step 3
Consider the moments about $O_4$.
\[\begin{align*} \sum \mathbf{M}_{O4} = \mathbf{R}_{G4O4} \times (-m_4 \mathbf{A}_{G4}) + (-I_{G4} \mathbf{\alpha_4}) + \mathbf{R}_{CO_4} \times \mathbf{F}_C + \mathbf{R}_{BO4} \times \mathbf{F}_{34} = 0 \end{align*}\]to obtain
\[\begin{align*} \sum \mathbf{M}_{O4} = (-0.1318 F_{34x} + 0.0716 F_{34y} -40.4008) \hat{\mathbf{k}} \end{align*}\]Step 4
Combine Equations from Step 2 and Step 3 and solve $F_{34x}$ and $F_{34y}$.
\[\begin{align*} -0.0705 F_{34x} + 0.2084F_{34y} = - 19.9600\\ -0.1318 F_{34x} + 0.0716 F_{34y} = 40.4008 \end{align*}\]Solving these equations, we find:
\[\begin{align*} F_{34x} &= -311.7716 \ N\\ F_{34y} &= -9.7485 \ N \end{align*}\]Step 5
Calculate $F_{14}$ by considering the sum of forces on link 4
\[\begin{align*} \sum \mathbf{F}_i^4 = \mathbf{F}_{14} + \mathbf{F}_{34} + \mathbf{F}_C + (-m_4 \mathbf{A}_{G_4}) = 0 \end{align*}\]to give
\[\begin{align*} \mathbf{F}_{14} &= -\mathbf{F}_{34} - \mathbf{F}_C - (-m_4 \mathbf{A}_{G4})\\ \mathbf{F}_{14} &= -1.2073 \hat{\mathbf{i}} + 393.2992 \hat{\mathbf{j}} \ N \end{align*}\]Step 6
Calculate $F_{23}$ by summing the forces on link 3.
\[\begin{align*} \sum \mathbf{F}_{i3} = \mathbf{F}_{23} + \mathbf{F}_{43} +(-m_2\mathbf{A}_{G3}) \end{align*}\]to give
\[\begin{align*} \mathbf{F}_{23} &= -(-\mathbf{F}_{34}) - (-m_3 \mathbf{A}_{G3})\\ \mathbf{F}_{23} &= --241.8457 \hat{\mathbf{i}} + -242.1552\hat{\mathbf{j}} \ N \end{align*}\]Step 7
Calculate $\mathbf{F}_{12}$ by summing the forces on link 2
\[\begin{align*} \sum \mathbf{F}_{i2} &= \mathbf{F}_{12} + \mathbf{F}_{32} + (-m_2 \mathbf{A}_{G2}) \end{align*}\]to give
\[\begin{align*} \mathbf{F}_{12} &= - \mathbf{F}_{32} - 0 = \mathbf{F}_{23}\\ \mathbf{F}_{12} &= -241.8457 \hat{\mathbf{i}} - 242.1552 \hat{\mathbf{j}} \ N \end{align*}\]Step 8
Calculate the driving force $\mathbf{T}_{12}$ by summing the moment about point $O2$
\[\begin{align*} \sum \mathbf{M}_{O2} = \mathbf{R}_{AO2} \times \mathbf{F}_{32} + \mathbf{T}_{12} + (-I_{G2} \mathbf{\alpha}_2) \end{align*}\]to give
\[\begin{align*} \mathbf{T}_{12} &= -\mathbf{R}_{AO2} \times \mathbf{F}_{32} \\ &= 19.2916 \hat{\mathbf{k}}\ Nm \end{align*}\]