Velocity Analysis (Vector-Algebraic)

Fourbar Linkage Vector Loop Equations

The derivation of the vector loop equation for a fourbar linkage mechanism involves defining the position vectors of the links and the angles between them. The fourbar linkage consists of four links connected by four joints, forming a closed loop as shown in the figure below.

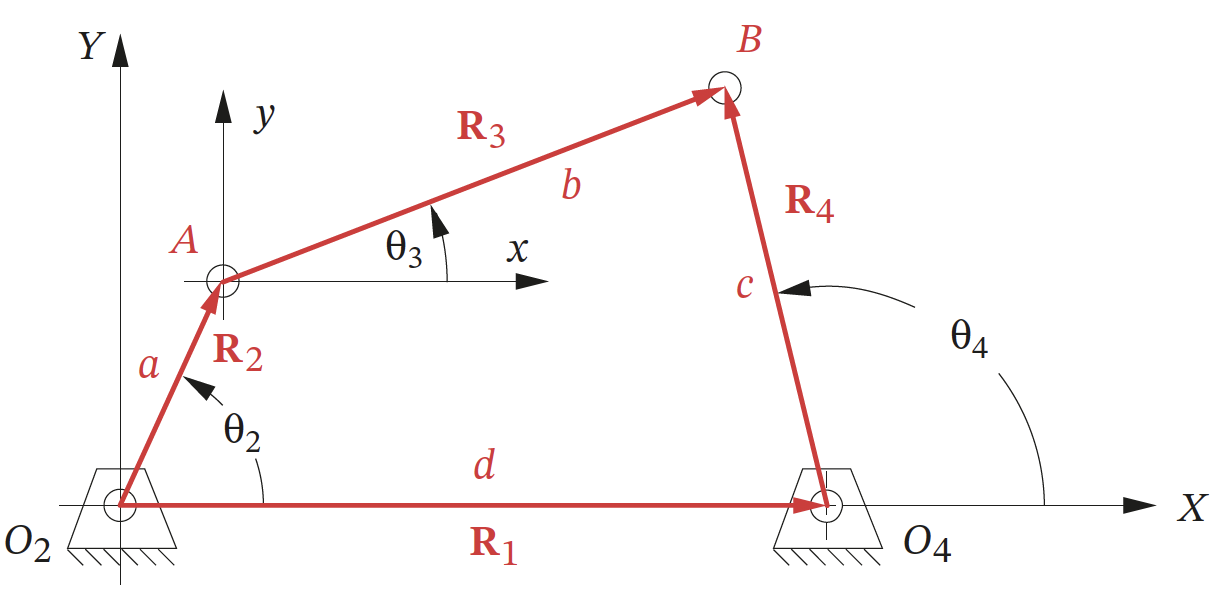
Vector Loop Equation

The vector loop equation is derived by summing the position vectors around the closed loop of the fourbar linkage and setting their sum to zero:

\[\mathbf{R}_{A} + \mathbf{R}_{BA} - \mathbf{R}_{BO4} - \mathbf{R}_{O4} = 0 \nonumber\]

To obtain an alternative form of the equations, often used in analysis, complex number notation can be used for the position vectors. Using complex notation, the following is obtained

\[a e^{j\theta_2} + b e^{j\theta_3} - c e^{j\theta_4} - d e^{j\theta_1} = 0 \nonumber\]

where $a$, $b$, $c$ and $d$ represent the scalar length of each of the links.

Euler’s equation, $e^{j\theta} = (\cos \theta + j \sin \theta)$ may also be substituted into the equations to obtain this form

\[\begin{align*} &a\left(\cos \theta_2 + j \sin \theta_2\right) + b\left(\cos \theta_3 + j \sin \theta_3\right) - \\ & c\left(\cos \theta_4 + j \sin \theta_4\right) - d\left(\cos \theta_1+j \sin \theta_1\right) = 0 \end{align*}\]

### Solving for Velocities

Determining velocities from the vector loop equation is a fairly simple process.

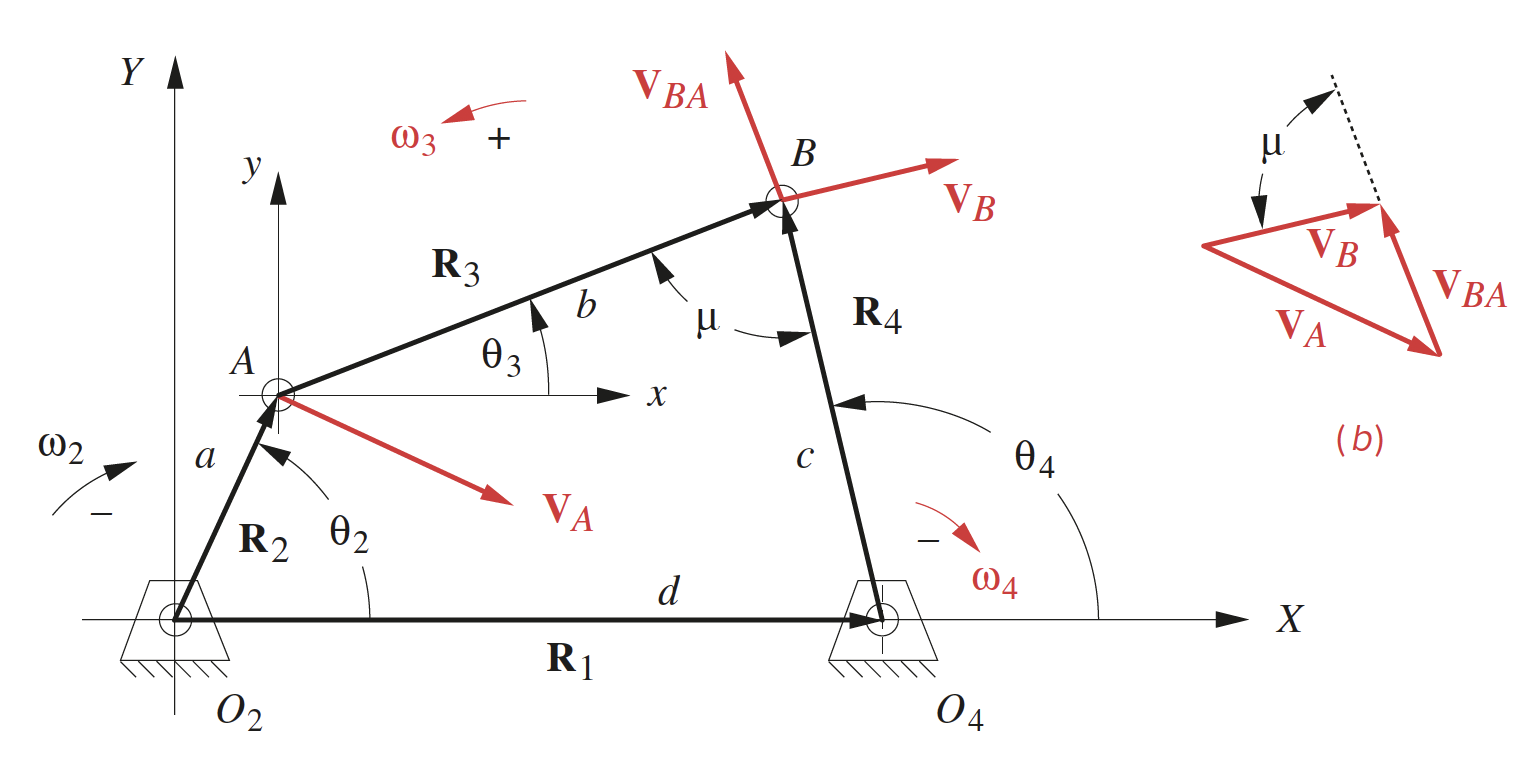
Differentiating the following equation from above

\[a e^{j\theta_2} + b e^{j\theta_3} - c e^{j\theta_4} - d e^{j\theta_1} = 0 \nonumber\]

with respect to time.

\[j a e^{j \theta_2} \frac{d \theta_2}{d t}+j b e^{j \theta_3} \frac{d \theta_3}{d t}-j c e^{j \theta_4} \frac{d \theta_4}{d t}=0 \label{eqa}\]

This equation is the velocity difference equation,

\[\mathbf{V_A}+\mathbf{V_{BA}-\mathbf{V_B}} \nonumber\]

where

\[\mathbf{V}_A = j a \omega_2 e^{j \theta_2} \\ \mathbf{V}_{B A} = j b \omega_3 e^{j \theta_3} \\ \mathbf{V}_B = j c \omega_4 e^{j \theta_4} \nonumber\]

noting the substition of $\frac{d \theta}{d t}=\omega$ in \ref{eqa}. The relative velocity equation may be written out in a different form

\[j a \omega_2 e^{j \theta_2}+j b \omega_3 e^{j \theta_3}-j c \omega_4 e^{j \theta_4}=0 \nonumber\]

The above can be solved to find $\omega_3$ and $\omega_4$ after some substitution and rearrangement. Firstly substitute the Euler identity, $e^{j\theta} = \cos(\theta) + j \sin(\theta)$ and then multiply through by $j$ to give,

\[a \omega_2\left(-\sin \theta_2+j \cos \theta_2\right)+b \omega_3\left(-\sin \theta_3+j \cos \theta_3\right) -c \omega_4\left(-\sin \theta_4+j \cos \theta_4\right)=0 \nonumber\]

separating the above into real and imaginary components, firstly the real part,

\[-a \omega_2 \sin \theta_2-b \omega_3 \sin \theta_3+c \omega_4 \sin \theta_4=0 \label{eq1}\]

and secondly the imaginary part.

\[a \omega_2 \cos \theta_2+b \omega_3 \cos \theta_3-c \omega_4 \cos \theta_4=0 \label{eq2}\]

Equations \ref{eq1} and \ref{eq2} can be solved simultaneously by direct substitution and the use of the identity $\sin \alpha-\beta = \cos \alpha \sin \beta - \cos \beta \sin \alpha$ to give.

\[\omega_3 = \omega_2 \frac{a}{b} \frac{\sin \left(\theta_4 - \theta_2\right)}{\sin \left(\theta_3 - \theta_4\right)} \\[1em] \omega_4 = \omega_2 \frac{a}{c} \frac{\sin \left(\theta_2 - \theta_3\right)}{\sin \left(\theta_4 - \theta_3\right)} \nonumber\]

Once $\omega_3$ and $\omega_4$ are known, it is possible to find $\mathbf{V_A}$, $\mathbf{V_{BA}}$ and $\mathbf{V_B}$.

\[\begin{align*} \mathbf{V_A} &=j a \omega_2\left(\cos \theta_2+j \sin \theta_2\right) \\ & = a \omega_2\left(-\sin \theta_2+j \cos \theta_2\right) \\[1em] \mathbf{V_{BA}} &= j b \omega_3\left(\cos \theta_3+j \sin \theta_3\right) \\ & = b \omega_3\left(-\sin \theta_3+j \cos \theta_3\right) \\[1em] \mathbf{V_B} & = j c \omega_4\left(\cos \theta_4+j \sin \theta_4\right) \\ &= c \omega_4\left(-\sin \theta_4+j \cos \theta_4\right) \nonumber \end{align*}\]

As can be seen from this, to find the velocities we need to know the positions $\theta_3$ and $\theta_4$. Given a value for $\theta_2$ as well as the length of each of the links, $a$, $b$, $c$ and $d$ we can find this using the methods previously discussed in Position Analysis.