Gruebler’s Equation
Understanding the number of degrees of freedom (DOF) a mechanism has is key for several reasons in kinematic analysis:
-
Motion Capabilities: The DOF indicates how many independent movements a mechanism can perform, which helps in understanding its control and potential actions.
-
Design Requirements: Knowing the DOF is crucial for aligning a mechanism’s design with its intended functions, especially in complex devices like robotic arms.
-
Control Complexity: More DOFs increase the complexity of controlling a mechanism, influencing the design of control systems and strategies.
-
Constraint Management: Analyzing how constraints affect DOF is vital for accurate design, ensuring mechanisms function as intended.
-
Simulation and Optimization: Accurate DOF knowledge is essential for modelling mechanisms in software, predicting behaviour, and optimising performance.
-
Mechanism Synthesis: In creating new mechanisms, understanding required DOF aids in selecting or designing kinematic chains to meet specific motion needs.
In determining the number of degrees of freedom or mobility of a mechanism, the number of links and joints the mechanism has, and the interaction between them must be understood.
Thinking about planar mechanisms it is easy to understand that any unconnected link has 3 DOF, so that L links has 3L DOF. Two links will therefore have 6 DOF.
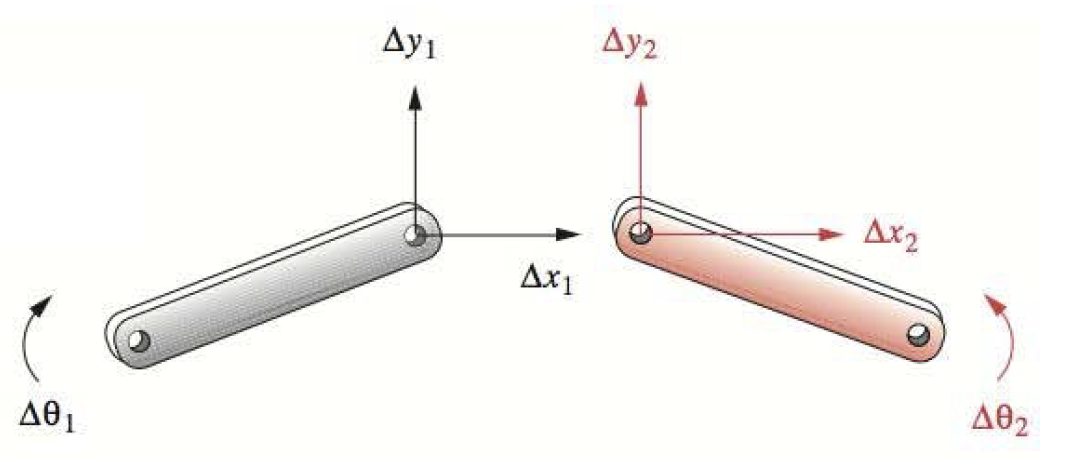
If the above 2 links are now connected through a full joint, this removes 2 DOF and the mechanism comprising the two links has 4 DOF.
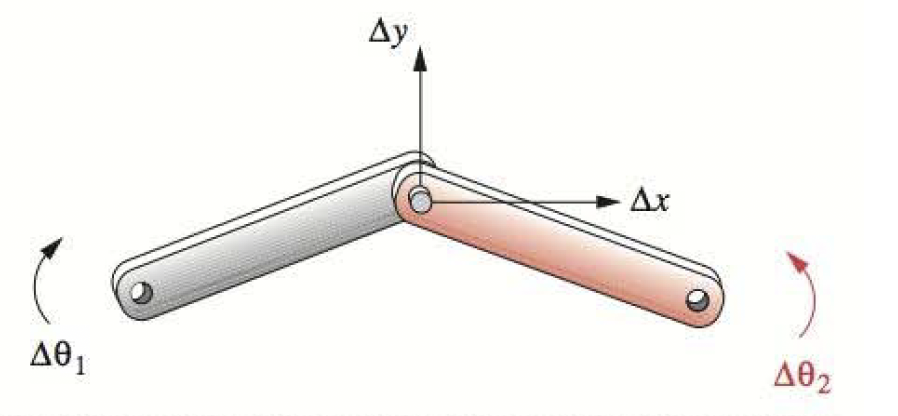
If the two links were instead connected through a half joint the mechanism would have 5 DOF since a half joint only removes 1 DOF.
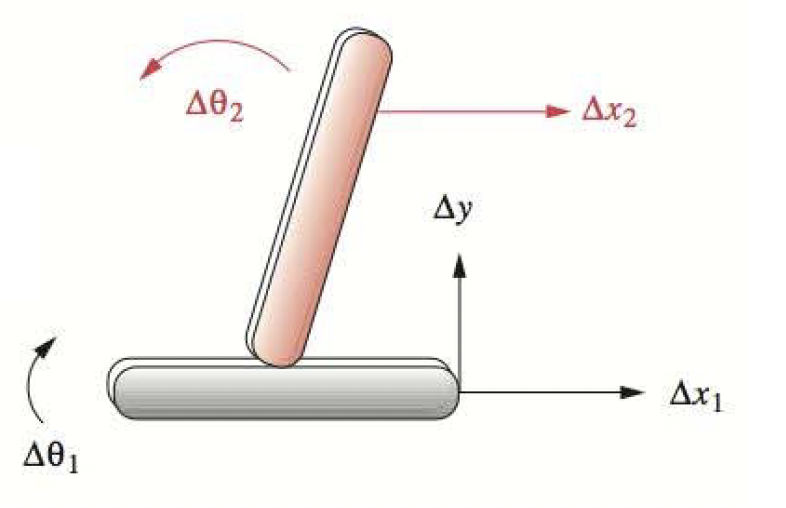
When a link is connected to ground, all degrees of freedom are removed.
Considering the above, it can be seen that the DOF of a mechanism or its mobility may be calculated using the following (Gruebler’s) equation.
\[M = 3L - 2J - 3G \nonumber\]where;
$M$ = degrees of freedom or mobility
$L$ = number of links
$J$ = number of joints
$G$ = number of grounded links
since, $G$ is always 1, this simplifies to;
\[M = 3(L - 1) - 2J \label{eq_1}\]In the above the value of $J$ must be equal to all of the joints in the mechanism, where half joints count as $\frac{1}{2}$, since they only remove 1 DOF. A modified version of the above equation can make it easier to take account of the type of link more explicitly.
\[M = 3(L - 1) - 2J_1 - J_2 \label{eq_2}\]where;
$J_1$ = number of 1DOF (full) joints
$J_2$ = number of 2DOF (half) joints
from the above it can be seen that, $2J = 2J_1 + J_2 $.
Examples
Considering the mechanism below.
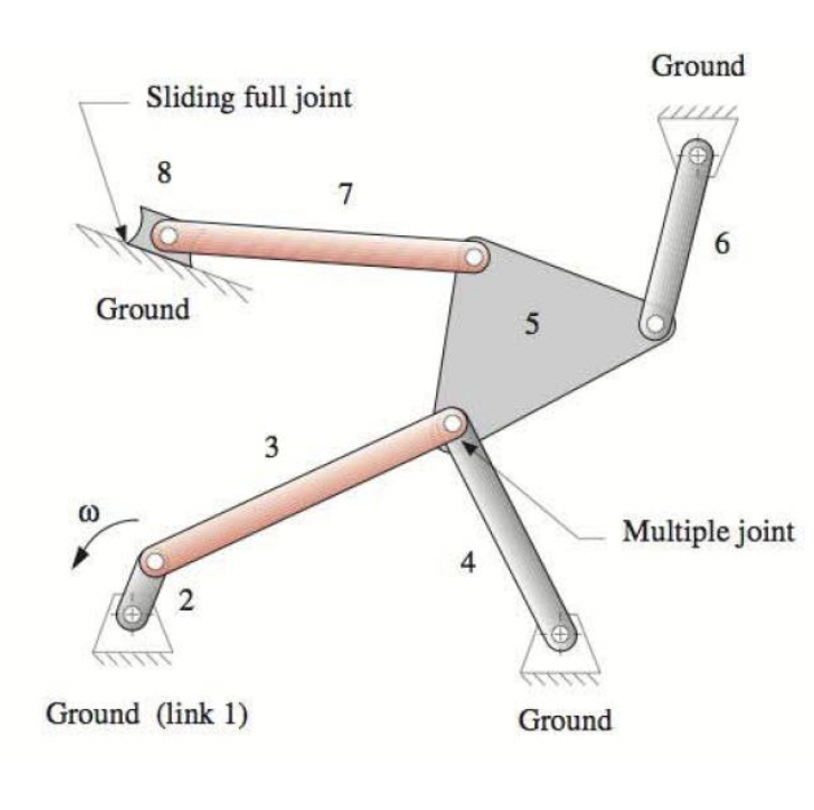
The total number of links (including ground), $L = 8$
The total number of joints, $J = 10$
The total number of 1DOF (full) joints, $J_1 = 10$
The total number of 2DOF (half) joints, $J_2 = 0$
So that using Equation $\ref{eq_1}$
\[\begin{align*} M &= 3(L - 1) - 2J \\ M &= 3(8 - 1) - 2 \cdot 10 \\ M & = 1 \end{align*}\]and using Equation $\ref{eq_2}$
\[\begin{align*} M &= 3(L - 1) - 2J_1 - J_2 \\ M &= 3(8 - 1) - 2\cdot10 - 0\\ M & = 1 \end{align*}\]Considering the mechanism below.
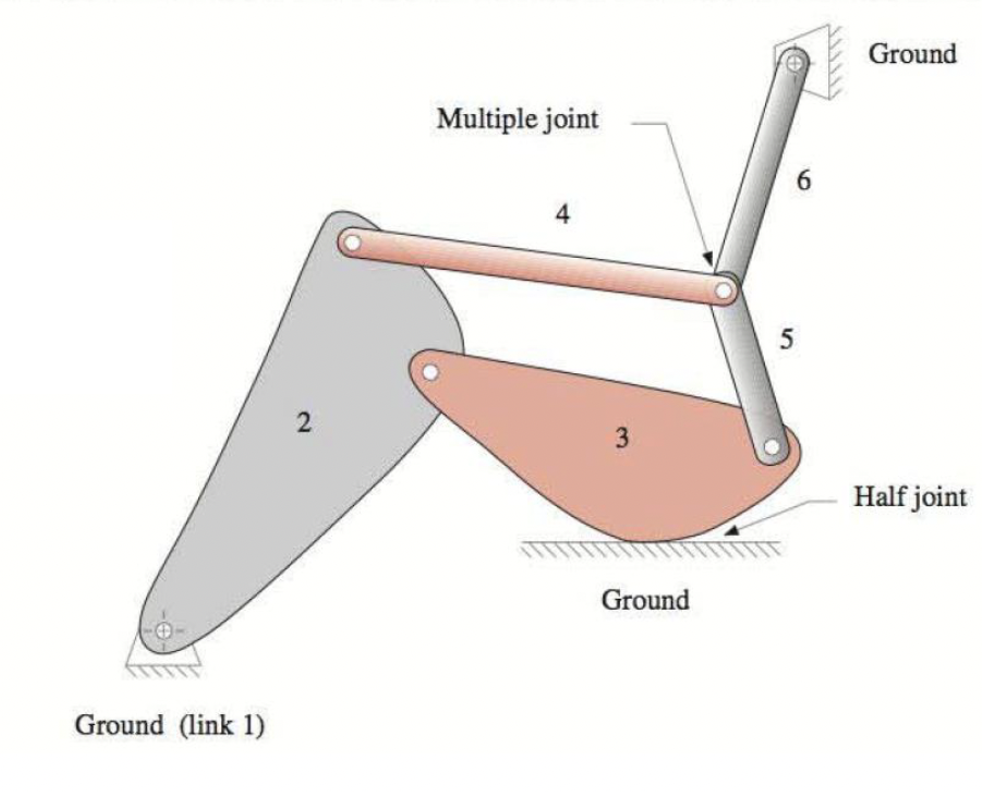
The total number of links (including ground), $L = 6$
The total number of joints, $J = 7.5$
The total number of 1DOF (full) joints, $J_1 = 7$
The total number of 2DOF (half) joints, $J_2 = 1$
So that using Equation $\ref{eq_1}$
\[\begin{align*} M &= 3(L - 1) - 2J \\ M &= 3(6 - 1) - 2 \cdot 7.5 \\ M & = 0 \end{align*}\]and using Equation $\ref{eq_2}$
\[\begin{align*} M &= 3(L - 1) - 2J_1 - J_2 \\ M &= 3(6 - 1) - 2 \cdot 7 - 1\\ M &= 0 \end{align*}\]