Week 2 Tutorial - Kinematic Analysis of Mechanisms
Question 1
Use ChatGTP to create some MATLAB code to find the values of $A_x$, $A_y$, $B_x$, $B_y$, $\theta_3$ and $\theta_4$ based on the analytical approach for the fourbar linkage mechanism whose details are shown below. Use the notes provided on the fourbar linkage mechanism analytical solution for position analysis found here
| Parameter | Value |
|---|---|
| a | 5 |
| b | 4 |
| c | 7 |
| d | 6 |
| θ₂ | 30° |
Once you have some working code ask ChatGTP to modify the code to make an assessment of whether the linkage is feasible given the parameters provided and only perform the calculation of $A_x$, $A_y$, $\theta_3$ and $\theta_4$ if the mechanism is feasible.
Find some values of a, b, c and d that make the mechanism feasible and unfeasible.
Example Solution
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
% Given parameters
a = 5;
b = 4;
c = 7;
d = 6;
theta_2 = 30; % in degrees
% Convert theta_2 to radians
theta_2_rad = deg2rad(theta_2);
% Calculate coordinates of point A
A_x = -a * cos(theta_2_rad);
A_y = a * sin(theta_2_rad);
% Calculate intermediate values
S = (a^2 - b^2 + c^2 - d^2) / (2 * (A_x - d));
P = (A_y^2 / (A_x - d)^2) + 1;
Q = (2 * A_y * (d - S)) / (A_x - d);
R = (d - S)^2 - c^2;
% Calculate positions of point B_y
discriminant = sqrt(Q^2 - 4 * P * R);
B_y1 = (-Q + discriminant) / (2 * P);
B_y2 = (-Q - discriminant) / (2 * P);
% Check if roots are complex
if isreal(B_y1) && isreal(B_y2)
fprintf('The roots are real. The mechanism is feasible for the given parameters.\n');
% Calculate B_x if roots are real
B_x = (a^2 - b^2 + c^2 - d^2) / (2 * (A_x - d)) - (2 * A_y * B_y1) / (2 * (A_x - d));
% Calculate angles theta_3 and theta_4
theta_3 = atan2d(B_y1 - A_y, B_x - A_x); % in degrees
theta_4 = atan2d(B_y1, B_x - d); % in degrees
% Display results
fprintf('Position of A:\n');
fprintf('A_x = %.2f\n', A_x);
fprintf('A_y = %.2f\n\n', A_y);
fprintf('Position of B:\n');
fprintf('B_x = %.2f\n', B_x);
fprintf('B_y1 = %.2f\n', B_y1);
fprintf('B_y2 = %.2f\n', B_y2);
fprintf('Angles theta_3 and theta_4 for B_y1:\n');
fprintf('theta_3 = %.2f degrees\n', theta_3);
fprintf('theta_4 = %.2f degrees\n\n', theta_4);
else
fprintf('The roots are complex. The mechanism is infeasible for the given parameters.\n');
end
Question 2
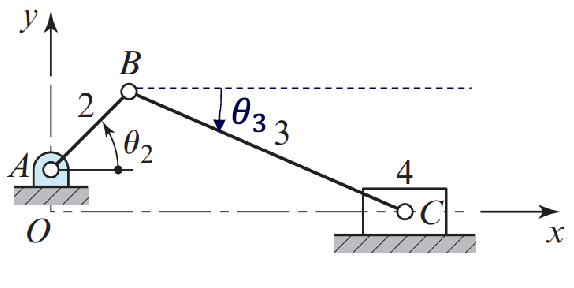
Given the slider-crank linkage (driven by the crank link 2) shown in the figure above, find the position of Slider 4 as function of $\theta_2$. Link dimensions are $R_{AO}$ = 20 mm, $R_{BA}$ = 50 mm and $R_{CB}$ = 140 mm.
Solution
Step 1: Define the Variables of the Problem
\[\mathbf{R}_{A0}, \ \mathbf{R}_{BA}, \ \mathbf{R}_{CB}, \ \mathbf{R}_C, \ \theta_2 \text{ and } \theta_3 \nonumber\]Step 2: Write the Vector Loop Equation
\[\mathbf{R}_{A0}+\mathbf{R}_{B A}+\mathbf{R}_{C B}=\mathbf{R}_C \nonumber\]Step 3: Use Complex Exponential Form
Using complex exponential form where, $R_{A0} = |\mathbf{R}_{A0}|$ and substitute Euler’s formula.
\[\begin{align*} R_{A0} e^{j\frac{\pi}{2}} = R_{A0} (\cos \frac{\pi}{2} + j \sin \frac{\pi}{2}) = j R_{A0} \\ R_{BA} e^{j\theta_2} = R_{BA} (\cos \theta_2 + j \sin \theta_2) \\ R_{CB} e^{j\theta_3} = R_{CB} (\cos \theta_3 + j \sin \theta_3) \end{align*}\]Noting that since $\mathbf{R}_{A0}$ is fixed vertical to the origin 0, at an angle $\pi/2$. So that,
\[R_C = j R_{A0} + R_{BA} (\cos \theta_2 + j \sin \theta_2) + R_{CB} (\cos \theta_3 + j \sin \theta_3) \nonumber\]Step 4: Separate Real and Imaginary Parts
Separate the vector equation into real and imaginary parts:
\[\begin{align*} R_C &= R_{BA} \cos \theta_2 + R_{CB} \cos \theta_3 \\ 0 &= R_{A0} + R_{BA} \sin \theta_2 + R_{CB} \sin \theta_3 \end{align*}\]Step 5: Solve for $\theta_3$
From the imaginary part, solve for $\theta_3$:
\[\begin{align*} &R_{A0} + R_{BA} \sin \theta_2 + R_{CB} \sin \theta_3 = 0 \\ &\sin \theta_3 = \frac{-R_{A0} - R_{BA} \sin \theta_2}{R_{CB}} \\ &\theta_3 = \sin^{-1}\left(\frac{-R_{A0} - R_{BA} \sin \theta_2}{R_{CB}}\right) \end{align*}\]Step 6: Solve for $ R_C $
Substitute $ \theta_3 $ into the real part to solve for $ R_C $:
\[\begin{align*} R_C&=R_{B A} \cos \theta_2+R_{C B} \cos \theta_3 \\ R_C&=R_{B A} \cos \theta_2+R_{C B} \cos \left(\sin^{-1}\left(\frac{-R_{A0} - R_{BA} \sin \theta_2}{R_{CB}}\right)\right) \end{align*}\]From our knowledge of trigonomic identities, $\cos(\sin^{-1} x) = \sqrt{1 - x^2}$ we can simplify the expression above.
\(\begin{align*} R_C &= R_{B A} \cos \theta_2+R_{C B} \sqrt{1 - \left(\frac{-R_{A0} - R_{BA} \sin \theta_2}{R_{CB}}\right)^2} \\ R_C &= R_{B A} \cos \theta_2+R_{C B} \sqrt{\frac{R_{CB}^2 - \left({R_{A0} + R_{BA} \sin \theta_2}\right)^2}{R_{CB}^2}} \\ R_C &= R_{B A} \cos \theta_2+\sqrt{R_{CB}^2 - \left(R_{A0} + R_{BA} \sin \theta_2\right)^2} \\ R_C &= 50 \cos \theta_2 + \sqrt{19200 - 1000 \sin \theta_2 - 2500 \sin^2 \theta_2} \end{align*}\)
Question 3
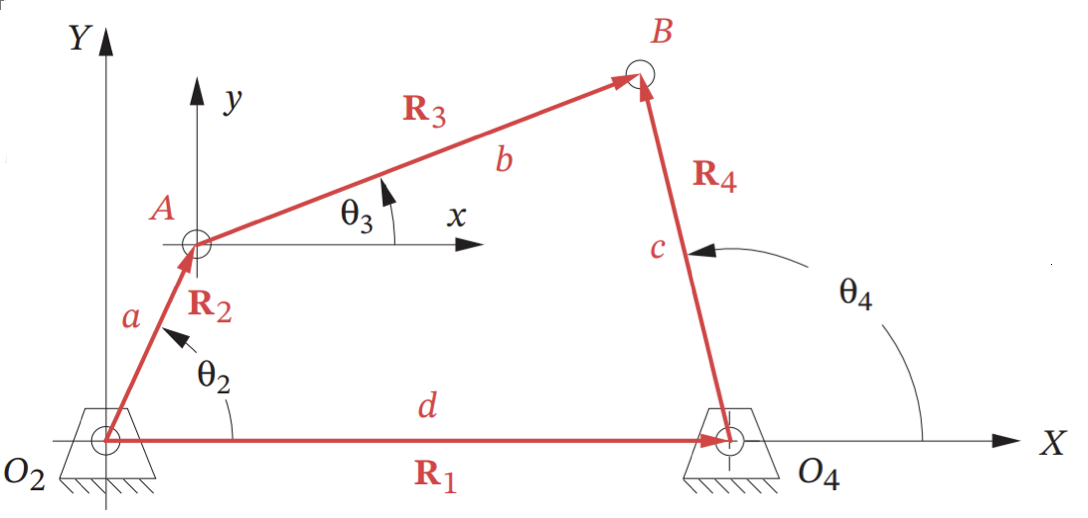
Given the four-bar linkage with the following information, find the value of $\alpha_3$, $\alpha_4$ and the acceleration of $A_A$, $A_{BA}$ and $A_B$.
| Parameter | Value |
|---|---|
| d | 100 mm |
| a | 40 mm |
| b | 120 mm |
| c | 80 mm |
| θ₂ | 40° |
| ω₂ | 25 rad/s |
| α₂ | 15 rad/s² |
Solution
Step 1
Determine the angles $\theta_3$ and $\theta_4$ according to Fourbar Link Mechanism Position Analysis
Step 2
Determine the angular velocities of $\omega_3$ and $\omega_4$ according to Fourbar Link Mechanism Velocity Analysis
Step 3
Determine the angular velocities of $\alpha_3$ and $\alpha_4$ according to Fourbar Link Mechanism Acceleration Analysis
Step 4
Determine the velocities of $A_A$, $A_{BA}$ and $A_B$ according to Fourbar Link Mechanism Acceleration Analysis
Step 5
Check your solutions
| Parameter | Solution |
|---|---|
| $\theta_3$ | $20.3^o$ |
| $\theta_4$ | $57.33^o$ |
| $\omega_3$ | $−4.12 \ rad/s$ |
| $\omega_4$ | $7.00 \ rad/s$ |
| $\alpha_3$ | $-322.46 \ rad/s^2$ |
| $\alpha_4$ | $-470.13 \ rad/s^2$ |
| $A_{Ax}$ | $-19.54 \ m/s^2$ |
| $A_{Ay}$ | $-15.61 \ m/s^2$ |
| $A_{BAx}$ | $11.51 \ m/s^2$ |
| $A_{BAy}$ | $-37.00 \ m/s^2$ |
| $A_{Bx}$ | $-33.77 \ m/s^2$ |
| $A_{By}$ | $17.01 \ m/s^2$ |