Position Analysis (Vector-Algebraic)

Fourbar Linkage Vector Loop Equations

The derivation of the vector loop equation for a fourbar linkage mechanism involves defining the position vectors of the links and the angles between them. The fourbar linkage consists of four links connected by four joints, forming a closed loop as shown in the figure below.

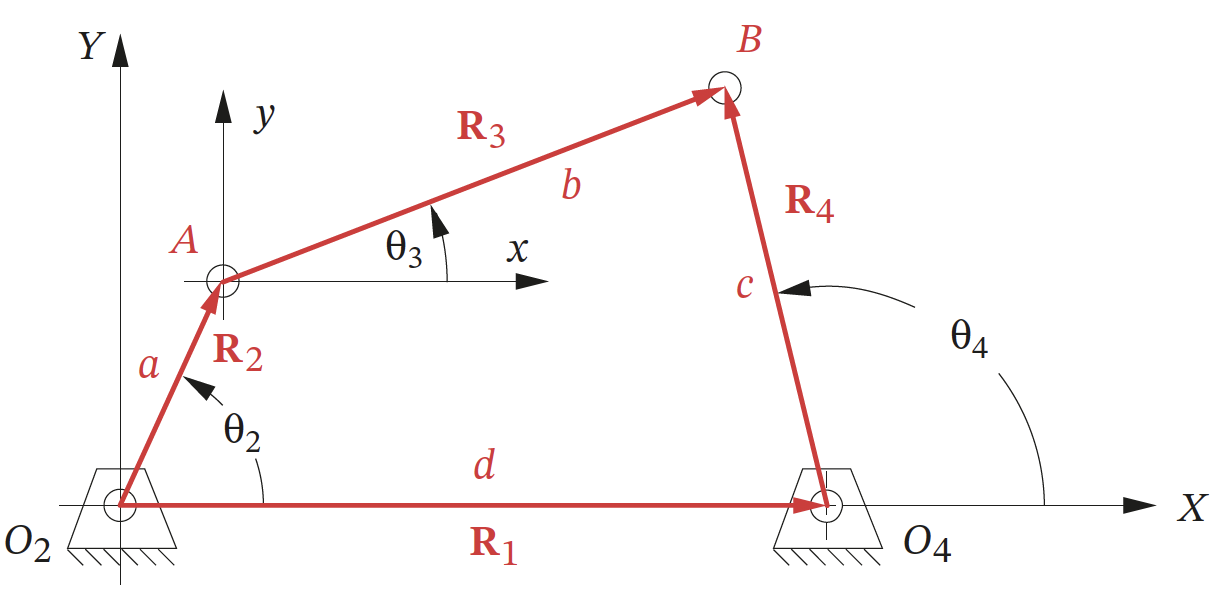
Vector Loop Equation

The vector loop equation is derived by summing the position vectors around the closed loop of the fourbar linkage and setting their sum to zero:

\[\mathbf{R}_{A} + \mathbf{R}_{BA} - \mathbf{R}_{BO4} - \mathbf{R}_{O4} = 0 \nonumber\]

To obtain an alternative form of the equations, often used in analysis, complex number notation can be used for the position vectors. Using complex notation, the following is obtained

\[a e^{j\theta_2} + b e^{j\theta_3} - c e^{j\theta_4} - d e^{j\theta_1} = 0 \nonumber\]

where $a$, $b$, $c$ and $d$ represent the scalar length of each of the links.

Euler’s equation, $e^{j\theta} = (\cos \theta + j \sin \theta)$ may also be substituted into the equations to obtain this form

\[\begin{align*} &a\left(\cos \theta_2 + j \sin \theta_2\right) + b\left(\cos \theta_3 + j \sin \theta_3\right) - \\ & c\left(\cos \theta_4 + j \sin \theta_4\right) - d\left(\cos \theta_1+j \sin \theta_1\right) = 0 \end{align*}\]

Solving the Vector Loop Equation

Taking the equation above and separating the real and imaginary components, the following equations are obtained

Real part (x component):

\[a \cos \theta_2 + b \cos \theta_3 - c \cos \theta_4 - d = 0 \label{eq1}\]

Imaginary part (y component):

\[a \sin \theta_2 + b \sin \theta_3 - c \sin \theta_4 = 0 \label{eq2}\]

noting that $\theta_1 = 0$. Equations \ref{eq1} and \ref{eq2} can be solved simultaneously to find $\theta_4$.

Squaring both equations, adding and rearranging.

\[\begin{align*} &b^{2} \left(\sin^{2}{\left(\theta_{3} \right)} + \cos^{2}{\left(\theta_{3} \right)}\right) = \left(- a \sin{\left(\theta_{2} \right)} + c \sin{\left(\theta_{4} \right)}\right)^{2} + \\ & \quad \left(- a \cos{\left(\theta_{2} \right)} + c \cos{\left(\theta_{4} \right)} + d\right)^{2}\\[1em] &b^{2} \left(\sin^{2}{\left(\theta_{3} \right)} + \cos^{2}{\left(\theta_{3} \right)}\right) = a^{2} \left(\sin^{2}{\left(\theta_{2} \right)} + \cos^{2}{\left(\theta_{2} \right)}\right) + \\ & \quad a \left(- 2 c \sin{\left(\theta_{2} \right)} \sin{\left(\theta_{4} \right)} - 2 c \cos{\left(\theta_{2} \right)} \cos{\left(\theta_{4} \right)} - 2 d \cos{\left(\theta_{2} \right)}\right) + \\ & \quad c^{2} \left(\sin^{2}{\left(\theta_{4} \right)} + \cos^{2}{\left(\theta_{4} \right)}\right) + 2 c d \cos{\left(\theta_{4} \right)} + d^{2} \end{align*}\]

noting that $(\sin^2 \theta_3+\cos^2 \theta_3) = 1$, which reduces the above to

\[\begin{align*} & b^{2} = a^{2} - 2 a c \sin{\left(\theta_{2} \right)} \sin{\left(\theta_{4} \right)} - 2 a c \cos{\left(\theta_{2} \right)} \cos{\left(\theta_{4} \right)} - \\ & \quad 2 a d \cos{\left(\theta_{2} \right)} + c^{2} + 2 c d \cos{\left(\theta_{4} \right)} + d^{2} \end{align*}\]

Rearrange and divide through by $2 a c$ to get,

\[\begin{align*} & - \sin{\left(\theta_{2} \right)} \sin{\left(\theta_{4} \right)} - \cos{\left(\theta_{2} \right)} \cos{\left(\theta_{4} \right)} - \frac{d \cos{\left(\theta_{2} \right)}}{c} + \\ & \qquad\frac{d \cos{\left(\theta_{4} \right)}}{a} + \frac{a^{2} - b^{2} + c^{2} + d^{2}}{2 a c} \end{align*}\]

using half angle identities

\[\sin \theta_4=\frac{2 \tan \left(\frac{\theta_4}{2}\right)}{1+\tan ^2\left(\frac{\theta_4}{2}\right)} ; \quad \cos \theta_4=\frac{1-\tan ^2\left(\frac{\theta_4}{2}\right)}{1+\tan ^2\left(\frac{\theta_4}{2}\right)} \nonumber\]

the expression becomes

\[\begin{align*} &- \frac{\left(1 - \tan^{2}{\left(\frac{\theta_{4}}{2} \right)}\right) \cos{\left(\theta_{2} \right)}}{\tan^{2}{\left(\frac{\theta_{4}}{2} \right)} + 1} - \frac{2 \sin{\left(\theta_{2} \right)} \tan{\left(\frac{\theta_{4}}{2} \right)}}{\tan^{2}{\left(\frac{\theta_{4}}{2} \right)} + 1} - \frac{d \cos{\left(\theta_{2} \right)}}{c} + \\ & \quad \frac{d \left(1 - \tan^{2}{\left(\frac{\theta_{4}}{2} \right)}\right)}{a \left(\tan^{2}{\left(\frac{\theta_{4}}{2} \right)} + 1\right)} + \frac{a^{2} + - b^{2} + c^{2} + d^{2}}{2 a c}\\[1em] \end{align*}\]

multiplying by $1 + \tan^2(\frac{\theta_4}{2})$

\[\begin{align*} &- \left(1 - \tan^{2}{\left(\frac{\theta_{4}}{2} \right)}\right) \cos{\left(\theta_{2} \right)} - 2 \sin{\left(\theta_{2} \right)} \tan{\left(\frac{\theta_{4}}{2} \right)} - \frac{d \left(\tan^{2}{\left(\frac{\theta_{4}}{2} \right)} + 1\right) \cos{\left(\theta_{2} \right)}}{c} + \\ & \quad \frac{d \left(1 - \tan^{2}{\left(\frac{\theta_{4}}{2} \right)}\right)}{a} + \frac{\left(\tan^{2}{\left(\frac{\theta_{4}}{2} \right)} + 1\right) \left(a^{2} + - b^{2} + c^{2} + d^{2}\right)}{2 a c} \end{align*}\]

making substitutions for $K_1$, $K_2$ and $K_3$

\[\begin{align*} &K_{1} \left(1 - \tan^{2}{\left(\frac{\theta_{4}}{2} \right)}\right) - K_{2} \left(\tan^{2}{\left(\frac{\theta_{4}}{2} \right)} + 1\right) \cos{\left(\theta_{2} \right)} + \\ & \quad K_{3} \left(\tan^{2}{\left(\frac{\theta_{4}}{2} \right)} + 1\right) - \left(1 - \tan^{2}{\left(\frac{\theta_{4}}{2} \right)}\right) \cos{\left(\theta_{2} \right)} - 2 \sin{\left(\theta_{2} \right)} \tan{\left(\frac{\theta_{4}}{2} \right)} \end{align*}\]

where

\[\begin{align*} &K_1 = \frac{d}{a} \\[1em] &K_2 = \frac{d}{c} \\[1em] &K_3 = \frac{a^2 - b^2 + c^2 + d^2}{2 a c} \end{align*}\]

multiply out the brackets

\[\begin{split} & - K_{1} \tan^{2}{\left(\frac{\theta_{4}}{2} \right)} + K_{1} - K_{2} \cos{\left(\theta_{2} \right)} \tan^{2}{\left(\frac{\theta_{4}}{2} \right)} - K_{2} \cos{\left(\theta_{2} \right)} + \\ & \quad K_{3} \tan^{2}{\left(\frac{\theta_{4}}{2} \right)} + K_{3} - 2 \sin{\left(\theta_{2} \right)} \tan{\left(\frac{\theta_{4}}{2} \right)} + \cos{\left(\theta_{2} \right)} \tan^{2}{\left(\frac{\theta_{4}}{2} \right)} - \cos{\left(\theta_{2} \right)} \end{split}\]

Group terms involving $\tan(\frac{\theta_4}{2})$ and $\tan^2(\frac{\theta_4}{2})$

\[\begin{align*} &\left(- K_{1} - K_{2} \cos{\left(\theta_{2} \right)} + K_{3} + \cos{\left(\theta_{2} \right)}\right) \tan^{2}{\left(\frac{\theta_{4}}{2} \right)} - 2 \sin{\left(\theta_{2} \right)} \tan{\left(\frac{\theta_{4}}{2} \right)} + \\ & \quad K_{1} - K_{2} \cos{\left(\theta_{2} \right)} + K_{3} - \cos{\left(\theta_{2} \right)} \end{align*}\]

which is a quadratic in form

\[A \tan ^2\left(\frac{\theta_4}{2}\right)+B \tan \left(\frac{\theta_4}{2}\right)+C=0 \nonumber\]

where

\[\begin{aligned} & A=- K_{1} - K_{2} \cos{\left(\theta_{2} \right)} + K_{3} + \cos{\left(\theta_{2} \right)} \\ & B = - 2 \sin{\left(\theta_{2} \right)} \\ & C = K_{1} - K_{2} \cos{\left(\theta_{2} \right)} + K_{3} - \cos{\left(\theta_{2} \right)} \end{aligned}\]

So to find $\theta_4$ we use the quadratic formula

\[\begin{aligned} \theta_{4_{1,2}} & =2 \arctan \left(\frac{-B \pm \sqrt{B^2-4 A C}}{2 A}\right) \end{aligned}\]

To find $\theta_3$ we follow a similar procedure using Equations $\ref{eq1}$ and $\ref{eq2}$ but rearranged with $\theta_4$ on the left hand side.

\[\begin{align*} c \cos \theta_4 &= a \cos \theta_2 + b \cos \theta_3 - d \\ c \sin \theta_4 &= a \sin \theta_2 + b \sin \theta_3 \end{align*}\]

Squaring both equations, adding together and rearranging

\[\begin{align*} &c^2 \left( \sin^2 \theta_4 + \cos^2 \theta_4 \right) = \left(a \sin \theta_2 + b \sin \theta_3 \right)^2 +\\ & \quad \left( a \cos \theta_2 + b \cos \theta_3 - d \right)^2\\[1em] &c^{2} \left(\sin^{2}{\left(\theta_{4} \right)} + \cos^{2}{\left(\theta_{4} \right)}\right) = a^{2} \left(\sin^{2}{\left(\theta_{2} \right)} + \cos^{2}{\left(\theta_{2} \right)}\right) + \\ & \quad a \left(2 b \sin{\left(\theta_{2} \right)} \sin{\left(\theta_{3} \right)} + 2 b \cos{\left(\theta_{2} \right)} \cos{\left(\theta_{3} \right)} - 2 d \cos{\left(\theta_{2} \right)}\right) + \\ & \quad b^{2} \left(\sin^{2}{\left(\theta_{3} \right)} + \cos^{2}{\left(\theta_{3} \right)}\right) - 2 b d \cos{\left(\theta_{3} \right)} + d^{2} \end{align*}\]

noting that $(\sin^2 \theta+\cos^2 \theta) = 1$ which reduces the above to

\[\begin{align*} & c^{2} = a^{2} + 2 a b \sin{\left(\theta_{2} \right)} \sin{\left(\theta_{3} \right)} + 2 a b \cos{\left(\theta_{2} \right)} \cos{\left(\theta_{3} \right)} - \\ & \quad 2 a d \cos{\left(\theta_{2} \right)} + b^{2} - 2 b d \cos{\left(\theta_{3} \right)} + d^{2} \end{align*}\]

rearrange and divide through by $2 a b$ to get

\[\begin{align*} & -\sin{\left(\theta_{2} \right)} \sin{\left(\theta_{3} \right)} - \cos{\left(\theta_{2} \right)} \cos{\left(\theta_{3} \right)} + \frac{d \cos{\left(\theta_{2} \right)}}{b} + \\ & \quad \frac{d \cos{\left(\theta_{3} \right)}}{a} + \frac{-a^{2} - b^{2} + c^{2} - d^{2}}{2 a b} \end{align*}\]

using half angle identities

\[\sin \theta_4=\frac{2 \tan \left(\frac{\theta_3}{2}\right)}{1+\tan ^2\left(\frac{\theta_3}{2}\right)} ; \quad \cos \theta_4=\frac{1-\tan ^2\left(\frac{\theta_3}{2}\right)}{1+\tan ^2\left(\frac{\theta_3}{2}\right)} \nonumber\]

the expression becomes

\[\begin{align*} & - \frac{\left(1 - \tan^{2}{\left(\frac{\theta_{3}}{2} \right)}\right) \cos{\left(\theta_{2} \right)}}{\tan^{2}{\left(\frac{\theta_{3}}{2} \right)} + 1} - \frac{2 \sin{\left(\theta_{2} \right)} \tan{\left(\frac{\theta_{3}}{2} \right)}}{\tan^{2}{\left(\frac{\theta_{3}}{2} \right)} + 1} + \frac{d \cos{\left(\theta_{2} \right)}}{b} + \\ & \quad \frac{d \left(1 - \tan^{2}{\left(\frac{\theta_{3}}{2} \right)}\right)}{a \left(\tan^{2}{\left(\frac{\theta_{3}}{2} \right)} + 1\right)} + \frac{-a^{2} - b^{2} + c^{2} - d^{2}}{2 a b} \end{align*}\]

multiply by $1 + \tan^2(\frac{\theta_3}{2})$

\[\begin{align*} &-\left(1 - \tan^{2}{\left(\frac{\theta_{3}}{2} \right)}\right) \cos{\left(\theta_{2} \right)} - 2 \sin{\left(\theta_{2} \right)} \tan{\left(\frac{\theta_{3}}{2} \right)} + \frac{d \left(\tan^{2}{\left(\frac{\theta_{3}}{2} \right)} + 1\right) \cos{\left(\theta_{2} \right)}}{b} +\\ & \quad \frac{d \left(1 - \tan^{2}{\left(\frac{\theta_{3}}{2} \right)}\right)}{a} + \frac{\left(\tan^{2}{\left(\frac{\theta_{3}}{2} \right)} + 1\right) \left(-a^{2} - b^{2} + c^{2} - d^{2}\right)}{2 a b} \end{align*}\]

making substitutions for $K_1$, $K_4$ and $K_5$,

\[\begin{align*} & K_{1} \left(1 - \tan^{2}{\left(\frac{\theta_{3}}{2} \right)}\right) + K_{4} \left(\tan^{2}{\left(\frac{\theta_{3}}{2} \right)} + 1\right) \cos{\left(\theta_{2} \right)} + \\ & \quad K_{5} \left(\tan^{2}{\left(\frac{\theta_{3}}{2} \right)} + 1\right) - \left(1 - \tan^{2}{\left(\frac{\theta_{3}}{2} \right)}\right) \cos{\left(\theta_{2} \right)} - 2 \sin{\left(\theta_{2} \right)} \tan{\left(\frac{\theta_{3}}{2} \right)} \end{align*}\]

where

\[K_1 = \frac{d}{a}\\[1em] K_4 = \frac{d}{b}\\[1em] K_5 = \frac{c^2 - d^2 - a^2 - b^2}{2 a b} \nonumber\]

multiply out the brackets

\[\begin{align*} & -K_{1} \tan^{2}{\left(\frac{\theta_{3}}{2} \right)} + K_{1} + K_{4} \cos{\left(\theta_{2} \right)} \tan^{2}{\left(\frac{\theta_{3}}{2} \right)} + K_{4} \cos{\left(\theta_{2} \right)} + \\ &\quad K_{5} \tan^{2}{\left(\frac{\theta_{3}}{2} \right)} + K_{5} - 2 \sin{\left(\theta_{2} \right)} \tan{\left(\frac{\theta_{3}}{2} \right)} + \cos{\left(\theta_{2} \right)} \tan^{2}{\left(\frac{\theta_{3}}{2} \right)} - \cos{\left(\theta_{2} \right)} \end{align*}\]

Group terms involving $\tan(\frac{\theta_3}{2})$ and $\tan^2(\frac{\theta_3}{2})$

\[\begin{align*} & \left(- K_{1} + K_{4} \cos{\left(\theta_{2} \right)} + K_{5} + \cos{\left(\theta_{2} \right)}\right) \tan^{2}{\left(\frac{\theta_{3}}{2} \right)} - 2 \sin{\left(\theta_{2} \right)} \tan{\left(\frac{\theta_{3}}{2} \right)} + K_{1} + \\ & \quad K_{4} \cos{\left(\theta_{2} \right)} + K_{5} - \cos{\left(\theta_{2} \right)} \end{align*}\]

which is quadratic in form

\[D \tan^2\left(\frac{\theta_3}{2}\right) + E \tan\left(\frac{\theta_3}{2}\right) + F = 0 \nonumber\]

where

\[\begin{align*} &D = - K_{1} + K_{4} \cos{\left(\theta_{2} \right)} + K_5 + \cos{\left(\theta_{2} \right)}\\ &E = - 2 \sin{\left(\theta_{2} \right)}\\ &F = K_{1} + K_{4} \cos{\left(\theta_{2} \right)} + K_{5} - \cos{\left(\theta_{2} \right)} \end{align*}\]

so to find $\theta_3$ we use the quadratic formula

\[\theta_{3_{1,2}} = 2 \tan^{-1} \left( \frac{-E \pm \sqrt{E^2 - 4 D F}}{2 D} \right) \nonumber\]