Position Analysis (Algebraic Method)

Position analysis of linkages can be undertaken using an algebraic method, in this section a position analysis of a fourbar linkage mechanism is undertaken.

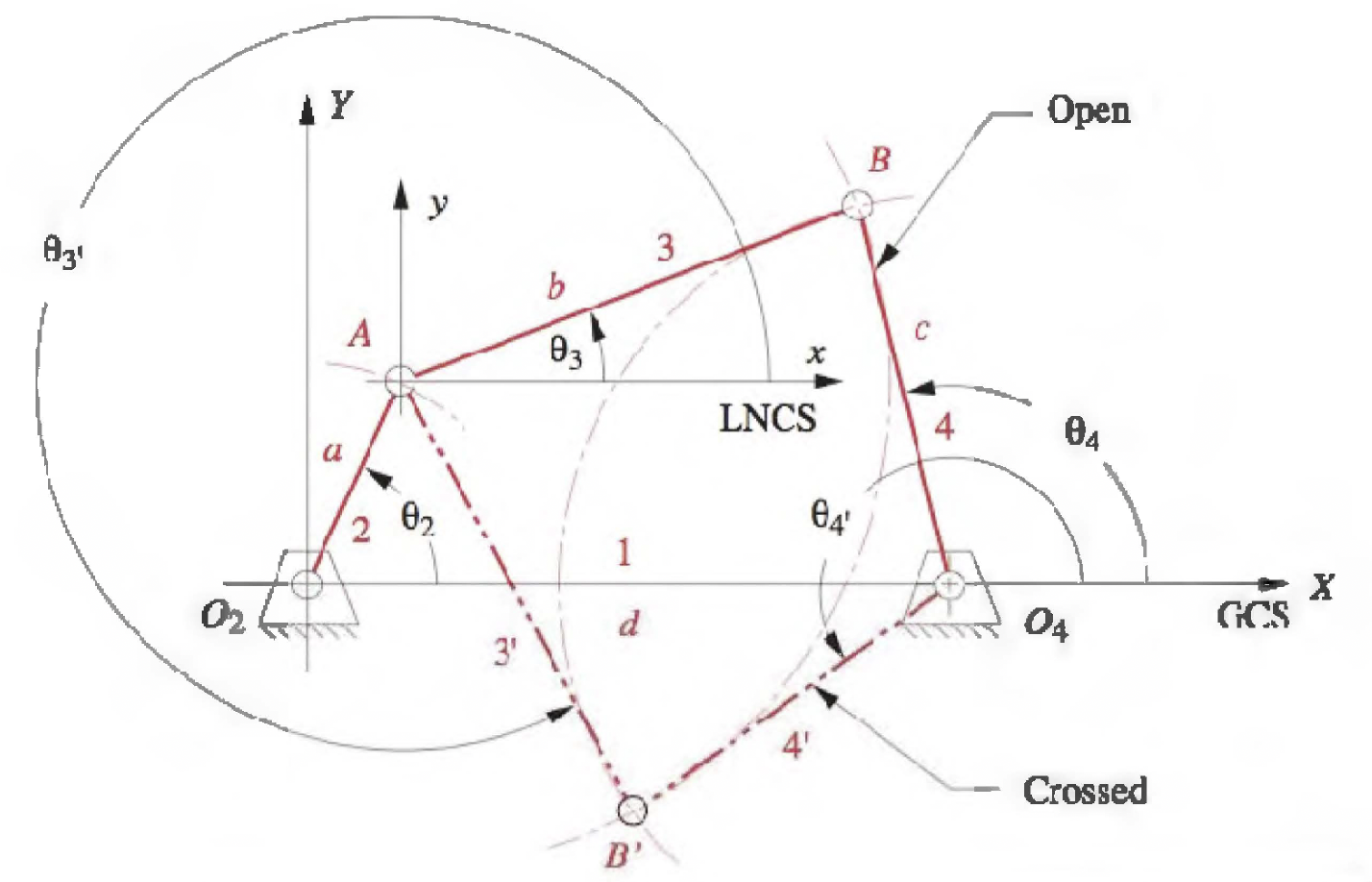
With reference to the figure above the coordinates of point $A$ are found using;

\[A_x=-a\cos{\theta_2}\\ A_y=a\sin{\theta_2} \nonumber\]

The coordinates of point B can be found from

\[\begin{align} b^2 &= (B_x-A_x)^2+(B_y-A_y)^2 \label{eq1}\\ c^2 &= (B_x-d)^2 + {B_y}^2 \label{eq2} \end{align}\]

this is a pair of simultaneous equations in $B_x$ and $B_y$. Subtracting \ref{eq2} from \ref{eq1} and rearranging gives

\[B_x=\frac{a^2-b^2+c^2-d^2}{2(A_x-d)}-\frac{2A_yB_y}{2(A_x-d)} \label{eq3}\]

substituting \ref{eq3} into \ref{eq2} gives a quadratic equation in $B_y$ which has two solutions

\[{B_y}^2+\left[\frac{a^2-b^2+c^2-d^2}{2(A_x-d)}-\frac{2A_yB_y}{2(A_x-d)}-d\right]^2-c^2=0 \nonumber\]

this can be solved with the quadratic formula

\[B_y=\frac{-Q \pm \sqrt{Q^2-4 P R}}{2 P} \nonumber\]

where

\[P=\frac{A_y^2}{\left(A_x-d\right)^2}+1 \\ Q=\frac{2 A_y(d-S)}{A_x-d} \\ R=(d-S)^2-c^2 \\ S=\frac{a^2-b^2+c^2-d^2}{2\left(A_x-d\right)} \nonumber\]

The solution i.e. roots, can be real or imaginary. If imaginary then this means that the mechanism is physically infeasible, an example of such a mechanism is one where with the dimensions given the links cannot connect with one another.

Once $B_y$ are known, \ref{eq3} can be used to calculate $B_x$. Following this the angles $\theta_3$ and $\theta_4$ can be calculated using the equations

\[\tan{\theta_3}=\left(\frac{B_y-A_y}{B_x-A_x}\right) \\ \tan{\theta_4}=\left(\frac{B_y}{B_x-d}\right) \nonumber\]